Část 1, Vědecké poznatky
Autor : Arie Otte (2017)
Obecně
Binokuláry s velkými zrcadly jsou poměrně vzácné a astro amatéry zajímají jejich výhody pro deep-sky pozorování. Toto často končí pouze jednou otázkou: jak velká jsou dvě zrcadla binokuláru ve srovnání s jedním, větším zrcadlem? Teoretická odpověď na tuto otázku je částečně závislá na kvantitativní hodnotě tzv. binokulárního součtového faktoru . V části 1 tohoto článku budu řešit historické a vědecké aspekty tohoto faktoru, stejně jako diskusi o jeho hodnotě a interpretaci. Z odborné literatury se pravidelně objevuje hodnota faktoru 1.4 až 1.7 x. Význam faktoru a jeho kvantitativní hodnota jsou často nesprávně interpretovány amatérskými astronomy.
Někdy je faktor 1.41 interpretován tak, jako kdyby člověk měl vynásobit průměr jediného zrcadla (nebo čočky) faktorem 1.41 pro výpočet ekvivalentního průměru binokuláru.
Jiný pohled však tvrdí, že je třeba vynásobit průměr jednoho zrcadla podstatně nižším faktorem √1.41 tj. 1.19 pro získání ekvivalentu dvou zrcadel. Tento rozdíl v interpretacích je z velké části kvůli nedostatku solidních údajů. Pro vyřešení této otázky jsem přímo porovnal 2 x 13 palců bino-dalekohled se 16-ti palcovým zrcadlovým dalekohledem. V druhé části článku budu popisovat výsledky, stejně jako porovnání dělané jinými pozorovateli. Rovněž budu popisovat relevanci binokulárního součtového faktoru v kontextu jiných aspektů binokulárního pozorování.
Úvod
Jak lze porovnávat velký zrcadlový bino-dalekohled s "mono-dalekohledem", který má významně větší zrcadlo? Majitele bino-dalekohledu může zaujmout vyšší poměr signálu k šumu, kterým dosáhne při pohledu přes binokulár, což vede ke zvýšení kontrastu obrazu. Zdá se však, že toto neposkytuje uspokojivou odpověď. Místo toho lidé, kteří nikdy nepoužili binokulár, prostě chtějí vědět, jak lze vypočítat ekvivalentní průměr dvou „binokulárových“ zrcadel. Tak například, pokud máte dvě 13 palcová zrcadla, součet ploch se rovná jednomu cca 18 palcovému zrcadlu. Ale co když vidíte s tímto 2 x 13 palcovým binokulárem jen tolik, jako s jedním 15 palcovým zrcadlem? Proč se pak obtěžujete binokulárem a jednoduše nekoupíte například 18 palcové zrcadlo, se kterým můžete vidět víc než se dvěma 13 palcovými zrcadly? Jde o oprávněné obavy, jelikož se jedná o spoustu peněz nebo o náročnou výrobu.
Zdánlivě logickým předpokladem by bylo, že "jedna plus jedna se rovná dvěma", což znamená, že můžete vidět dvakrát více dvěma očima než jedním okem. Malý pokus však ukazuje, že to nemůže být pravda. Když zavřete jedno oko během denního světla, je zřejmé, že stále vidíte více než 50% před uzavřením jednoho oka. Možná vidíte s jedním okem, stejně jako s dvěma očima, s výjimkou plochého obrazu, který je způsoben nepřítomností tzv. paralaxy. Teprve tehdy, když je obraz tmavý a objekty jsou viditelné na prahu viditelnosti, tak zaznamenáme rozdíl mezi prohlížením jedním nebo dvěma očima. Tento fenomén byl předmětem dlouhé historie výzkumu pozorování. Tento vědecký výzkum je částečně orientován zdravotně. Otázka je přirozeně důležitá v případech (částečného) oslepnutí na jedno oko způsobené nehodou nebo chorobou. Vedle těchto praktických, lékařských aspektů je také dlouhý a stálý zájem o teoretické aspekty "binokulárního" pozorování versus "monokulárního" pozorování. Část tohoto výzkumu se točí kolem otázky, jak lze kvantifikovat rozdíly ve sledování s jedním nebo dvěma očima. V mnoha kvantitativních modelech hraje binokulární součtový faktor a jeho kvantitativní hodnota důležitou roli.
Binokulární součtový faktor
Binokulární součet je proces, kterým mozek kombinuje informace, které dostává příchozími signály z levého a pravého oka. Pomocí binokulárního součtu je prahová hodnota pro detekci slabých objektů nižší u dvou očí než u jednoho oka. Statisticky existuje výhoda pro detekci slabého signálu při použití dvou detektorů místo jednoho detektoru. Tato výhoda je √2 tedy 1.41, nazývaná binokulární součtový faktor . Na webových stránkách Bruce Sayre je citována skvělá přednáška dr. Thomas Salmona. V této přednášce je shrnuta tato teorie.
Dřívější experimenty se snažily určit kvantitativně výhodu binokulárního pozorování (Pirenne, 1943). Bylo zjištěno, že při binokulární detekci je slabý světelný signál 1.4 násobně lepší než při monokulární detekci. Teorie, která byla založena na těchto prvních pokusech, se nazývá teorie pravděpodobnosti součtu . Pro představu, jak byly tyto experimenty provedeny a vysvětleny, shrnu některé z těchto zjištění. Pirenne používal záblesky světla s různým jasem po dobu trvání několika milisekund. Pozorovaná frekvence spatření záblesku světla byla pozorována u levého oka, pak jen pro pravé oko a následně pro obě oči. Zde je jeden příklad (Pirenne, 1943):
Naměřená frekvence spatření záblesku
Levé oko 25/125 = 0.198
Pravé oko 71/275 = 0.258
Obě oči 62/164 = 0.378 (1.66 lepší než je průměr levé / pravé oko)
Předpokládejme, že pravděpodobnost pozorování signálu levým okem (P l ) nebo pravým okem (P r ) je nezávisle lze předpokládat pravděpodobnost pozorování obou očí (P b ). Definice pravděpodobnosti detekce tohoto signálu oběma očima je: P b = P r + P l - (P r x P l ). Pokud výše uvedené pozorování pro levé a pravé oči jsou vypočteny, Pb = 0.198 + 0.258 - (0.198 x 0.258) = 0.405. To je docela blízko k pozorovanému 0.378. Jakmile jsou vykresleny výše uvedené a další experimentální údaje, dostaneme níže uvedený obrázek.
Křivka B se vypočte z hodnot pozorování levého (L) a pravého (R) oka. Při logaritmu jasu 1.0 je vykreslen výše popsaný příklad.
Je třeba si uvědomit pár věcí. Pozorované frekvence s oběma očima se blíží očekávané pravděpodobnosti, které byly vypočteny podle výše uvedeného vzorce. Proto se dospělo k závěru, že zvýšenou pravděpodobnost pozorování oběma očima (viz kroužky na obr. 1) lze vysvětlit pouze statistikou součtu a ne žádným jiným fyziologickým mechanismem fúze v mozku. Jinými slovy, obě oči jsou vnímány jako nezávislé detektory. Z toho vychází termín teorie pravděpodobnost součtu.
Druhá věc, kterou chci zdůraznit je, že křivky levého a pravého oka se výrazně liší. Ačkoli to lze očekávat u dvou různých očí s různou citlivostí atd., k tomuto bodu se vrátíme zpět později.

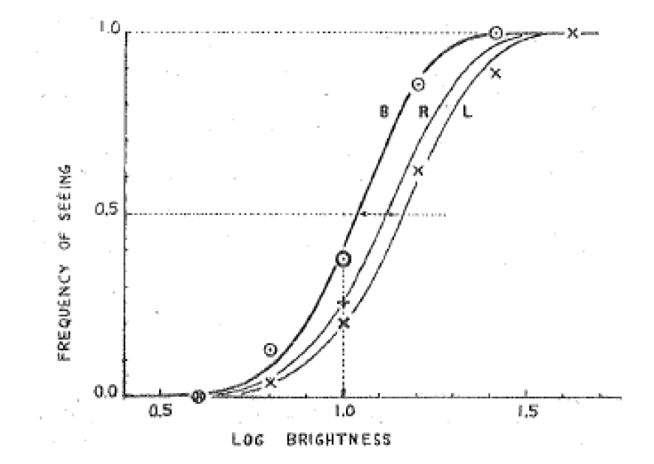
Obrázek 1. Experimentální data společnosti Pirenne, která odpovídají předpokládaným hodnotám pro větší pravděpodobnost pozorování blesku světla se dvěma očima (B) ve srovnání s pozorovanou frekvencí pozorováním pouze s levým (L) nebo pravým (R) okem. Kroužky, které leží na křivce B, jsou vypočtené hodnoty Pb.
Nakonec větší pravděpodobnost pozorování obou očí závisí na jasnosti podnětu. Salmon používal hodnotu pravděpodobnosti pozorování každým okem 0.6. To znamená, že celková pravděpodobnost pro dvě oči je 0.6 + 0.6 - (0.6 x 0.6) = 0.84. To je 1.4 krát více než 0.6, takže zde máme dříve citovaný √2 nebo 1.4 velký binokulární součtový faktor . Nicméně, pravděpodobnost detekce může být různá, v závislosti na tom, na co se člověk dívá. Pokud je to velmi obtížně viditelný objekt, pravděpodobnost detekce by byla velmi nízká, například 0.1. Pokud je objekt snadno viditelný, pravděpodobnost by byla téměř 1.0. V úvodu jsem se v této souvislosti zmínil o binokulárním pozorování za denního světla. Pokud se díváte za denního světla na jasný objekt, nezáleží na tom zda se na něho díváte s jedním nebo dvěma očima. Takže pravděpodobnost bude 1.0. To znamená, že celková pravděpodobnost pozorování u obou očí je také 1.0 (konkrétně 1.0 + 1.0 - (1.0 x 1.0) = 1.0). Tak to je jen při jasném světle, že pravděpodobnost pozorování s oběma očima bude vyšší. Pro případ, kdy pravděpodobnost každého oka je 0.3, pravděpodobnost pozorování u obou očí je 0.3 + 0.3 - (0.3 x 0.3) = 0.51. To je faktor 1.4 větší než pravděpodobnost pozorování pouze jedním okem. Tyto trendy jsou také viditelné na obrázku 1.
Obecně platí, že když vědci provádí experimenty s cílem stanovit prahovou hodnotu pro detekci, tak často používají hodnotu 0.5. Proč? Vzhledem k tomu, že není jasná úroveň intenzity, kterou můžete volat "prahovou hodnotu", běžně definují práh jako intenzitu, při které získáte 50% pravděpodobnost detekce, tedy 0.5. Pravděpodobnost, že dvě oči detekují signál, je nyní 0.5 + 0.5 - (0.5 x 0.5) = 0.75. A nyní máme nárůst o 1.5 násobek faktoru ve srovnání s 0.5 pravděpodobností pozorování pouze jedním okem.
Také často citovaný 1.4 binokulární součtový faktor je ve skutečnosti do značné míry závislý na tom, jak tmavé jsou pozorované objekty a často se používá jen z pohodlnosti. Je to proto, že se tato hodnota shoduje přesně s nárůstem průměru dvou kombinovaných zrcadlových ploch. Vezměte si například moje dvě zrcadla o průměru 13 palců. Povrch každého zrcadla je nebo π (1/2 x d)2 neboli ~ 132.6 palce. Součet povrchu obou zrcadel je tedy ~ 265.3 palce. A toto odpovídá jednomu zrcadlu o průměru ~ 18.4 palce. A to je přesně faktor √2 nebo 1.41 krát větší než moje 13 palcové zrcadlo.
Binokulární součet, binokulární snadnost a další aspekty binokulárního pozorování
Je známo, že mnoho vizuálních kortikálních neuronů je u vyšších primátů binokulárně spojeno. Od té doby existují funkční a fyzické interakce mezi vizuálními neurony z obou očí a je těžké uvěřit, že statistika a pravděpodobnost jsou jediným vysvětlením binokulárního součtu. Takže zatímco teorie součtu pravděpodobnosti je stále vnímána ve vědecké literatuře jako platný postup, existují další faktory, které ovlivňují hodnotu binokulárního součtového faktoru. Například existují podmínky, v nichž je nárůst binokulární citlivosti větší, než by bylo možné vysvětlit samotným součtem pravděpodobnosti. Optimální součet nastane, když 1) odpovídající body na obou sítnicích očí jsou stimulovány podobnými cíli nebo stimuly a 2) nebo když jsou podněty prezentovány oběma očím současně nebo nejméně v čase ~ 100 msec vzdáleném od sebe. V těchto případech je činnost mozku zvýšena více, než součtem obou aktivit v mozku, které jsou vybuzeny každým jedním okem zvlášť. Jestliže existuje nějaká výhoda nad uvedeným binokulárním součtovým faktorem 1.4, což se připisuje tomuto mechanismu, tak se nazývá binokulární facilitace neboli neurální součet .
Navíc Campbell a Green (1965) poskytli další vysvětlení, proč binokulární součet by měl být nižší než vizuální prahová hodnota s faktorem 1.4. Argumentují tím, že kombinace vstupních hodnot ze dvou oči, neurální signály by byly sečteny, zatímco pozadí, neurální šum (předpokládá se náhodný a nespojitý) by měl být částečně vyrušen. Předpověděli a měřili, že tento proces sám o sobě způsobit, že binokulární prahové hodnoty jsou nižší než faktor √2 neboli 1.4 (obrázek 2).
Proto je často opakované 1.4 násobné zlepšení vizuální funkce vysvětleno buď součtem pravděpodobnosti, tedy zvýšením poměru signálu k šumu nebo neurální součtem. Nějaké zlepšení o více než 1.4 násobek by znamenalo, že neurální součet, nebo nějaká jeho jiná forma, je zahrnuta do fyziologického součtu.
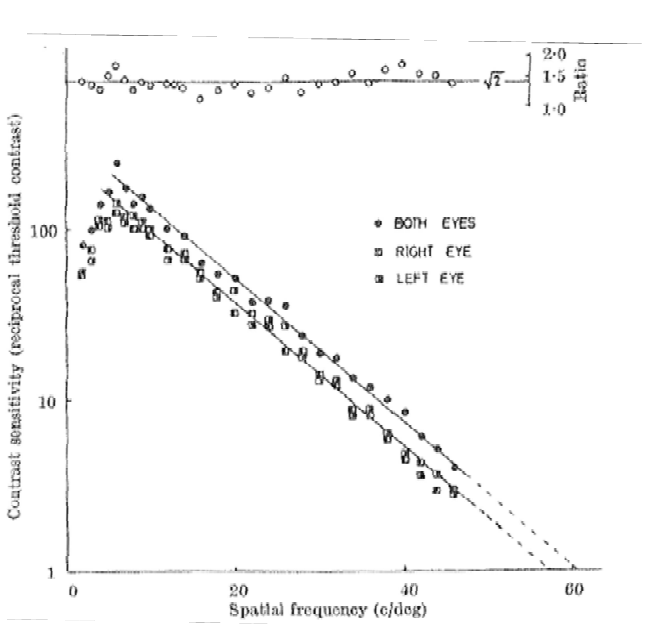

Obrázek 2. Testy citlivosti na kontrast Campbell a Green (1965). Prázdné kroužky nahoře reprezentují binokulární / (střední) monokulární citlivost. Rovná horizontální čára je průměr těchto poměrů v různých prostorových frekvencích, což je √2! (Ve skutečnosti 1.418 ± 0.021 pro tři pokusy se dvěma různými lidmi).
Od dob těchto orientačních studií bylo provedeno mnoho vědeckých výzkumů týkajícího se binokulárního oproti monokulárnímu pozorování. Bylo navrženo nejméně pět různých modelů (Meese a kol., 2006) k vysvětlení binokulárního součtu. Některé prováděné experimenty ukazují, že binokulární součet překračuje faktor √2 (Meese et al., 2006). Ve skutečnosti byly hlášeny faktory 1.4 až 2 (viz Frisen a Lindblom, 1988). Ale pokud mohu říci, dosud se neobjevila žádná jednoduchá interpretace. Existuje řada důvodů.
1. Metodologie se široce liší, což znamená, že není snadný úkol navrhnout experimenty, které by jednoznačně řešily a vyřešily problém správně. Jeden experiment může nechat adaptaci očí k tmavému předmětu po dobu 30 minut, v jiném experimentu mohou mít adaptace dobu pouhých 10 minut. V dalším pokusu, může být světlo tlumené pouze po dobu jedné sekundy, ale v jiném, po dobu 5 sekund. Tyhle všechny proměnné mohou ovlivnit výsledky a používané protokoly nejsou zdaleka standardizované. V mém případě
(viz níže) je důležité, že mé oči musí být dobře adaptované na tmu - tedy přizpůsobené k detekci nejslabší možné hvězdy. To obvykle trvá nejméně 15 až 30 minut.
2. Aspekty pozorování, jako je detekce prahových úrovní světla, kontrastu nebo rozlišení, jsou výhodou v binokulárním pozorování. Bodový zdroj by byl vnímán pouze malou plochou sítnice, ale větší zdroj by zahrnoval oblasti sítnice, které by mohly reagovat odlišně. Například, fyziologie centrálního 1 ° pozorování se velmi liší od několika stupňů periferního pozorování. Všechny tyto aspekty dělají "úpravu" binokulárního součtového faktoru složitější.
3. Naše dvě oči jsou zřídka kdy totožná, toto již lze vidět v datech z roku 1943 od Pirenneho. Faktor 1.41 může být platný pouze tehdy, jsou-li obě oči stejně citlivé a optimální. Ale v extrému to poklesne až na hodnotu 1, když jedno oko nemá vůbec žádnou citlivost (Nelson-Quigg, 2000).
4. V řadě studií jsou velké rozdíly mezi jednotlivci. Rozptyl je tak velký, že jedna studie dospěla k závěru, že možná vůbec neexistuje žádná konstanta binokulárního součtu (Frisen a Lindblom, 1988). Také dospěli k závěru, že stupeň binokulárního součtu souvisí se složitostí vizuální úlohy. Například, zjistili, že binokulární součet v testu rozlišení byl signifikantně menší než v detekčních testech. Podobně, když je složitější parametr, jako je kontrast, je odstraněn z výsledku binokulárního součtu a faktor je vyšší než často citovaný 1.4 (Meese a kol., 2006).
5. Říká se, že některé vědecké články používají přesné fráze, jako je "poměr √2" binokulární až monokulární kontrastní citlivost "(Anderson a Movskon, 1989). Nebo "binokulární součet (poměr binokulární k monokulární kontrastní prahové citlivosti) je ~ 1.4 "(Meese, 2006).
Interpretace binokulárního součtového faktoru amatérskými astronomy
Jak je amatéry vnímána hodnota √2 nebo vyšší pro faktor binokulárního součtu v astronomická komunita? Ve většině případů je argumentace jednoduchá: stačí přidat dvě plochy zrcadla. Jiní však říkají ne, tohle není způsob, jak věc funguje. Například Ed Zarenski na CloudyNights (Zarenski, 2006) uvádí: "tyto faktory se aplikují na průměr poskytující světlo každému oku, přičemž celková plocha obou otvorů nedodává světlo oběma očím. Mám na mysli tohle; nemůžete sečíst plochu dvou čoček o průměru 70 mm, 4900 + 4900 = 9800, pak √9800 vypočítat celkové světlo dodané se z ekvivalentního průměru otvoru 99 mm. Světlo je dodáváno z otvoru o průměru 70 mm na každé oko. Binokulární součtový faktory se aplikují na tento otvor 70 mm ".
Z toho vyplývá, že dvě čočky o průměru 70 mm nejsou ekvivalentní √ (A2 x 2) = √ (2 x 702) = √ (2 x 4900) = 99 mm. Místo toho se plocha 4900 krát násobí součtovým faktorem 1.41, který předpovídá hodnotu "nové" kombinované plocha pro dvě oči. Výsledkem je clona √ (4900 x1.41) = 83,2 mm, což je √2 násobek clony o průměru 70 mm. Ve vzorci se stává √ (A2 x 1.41) . Takže namísto násobení průměru zrcadla o √2, je průměr násoben faktorem √1.41 neboli 1,19. To by znamenalo, že moje zrcadla o rozměrech 2 x 13 palců jsou ekvivalentní ~ 15,5 palcového mono teleskopu místo ~ 18.3 palce.
Tato interpretace je omezena na amatérské astronomické publikum, které navštěvuje internetové fóra, jako je CloudyNights. Nicméně, toto bylo přijato širším publikem - Phil Harrington ve své knize Cosmic (Harrington, 2011). Přebírá interpretaci Zarenského a používá vzorec √ (A2x1.41). Využívá tento vzorec k výpočtu ekvivalentního průměru dalekohledu řady dalekohledů a jednoduše násobí průměr jednoho objektivu číslem 1.19.
Bez ohledu na to, který z těchto názorů je správný, je třeba si všimnout několika věcí:
1) Jak tvrdí, neexistuje žádná taková věc jako jediný binokulární součtový faktor. Jeho kvantitativní hodnota závisí například z velké části na tom, které parametry se používají pro čtení, jako je rozlišení, detekce apod. Faktor 1.41 je výsledkem často konvenčních předpokladů. Byla uváděna i hodnota faktoru 2. A faktor 2 by znamenal 1.41krát větší plochu binokuláru než u monokuláru o stejném průměru.
2) Pravděpodobně důležitější je otázka, zda lze přeložit binokulární součet poměrně lineárním způsobem, jak předpovídat srovnatelnou plochu jednoho zrcadla. Oční specialisté řeknou, nikdy se nepokoušejte o takové úsilí a mají důvod. Je velmi zjednodušené říci, co více nebo lépe vidíte dvěma očima než jedním okem. Z jejich perspektivy nedává smysl předkládat tuto otázku " jak velké by mělo být jedno oko, které bychom nahradili aby bylo ekvivalentní dvěma očím". Koneckonců, máme dvě oči, nikoli větší "Cyklop" oko, tak proč se obtěžovat s touto otázkou. Stručně řečeno, vezměme jakoukoliv hodnotu binokulárního součtového faktoru a použijme ho k předpovědi toho, jak velké srovnatelné mono-zrcadlo by mělo být, je interpretace významu faktoru. Vychází z pochopitelné posedlosti amatérských astronomů, kteří chtějí vědět, zda doslova stojí za to projít si problémem nákupu / výrobou bino-dalekohledu.
Vzhledem k těmto úvahám jsem začal pochybovat o poněkud jednorozměrném přístupu " existuje součtový faktor 1.41 a to znamená 1.19 zvýšení průměru " . Zvláště od té doby, co jsem měl dojem, že jsem viděl více s mým 2 x 13 palcovým bino-dalekohledem než bych mohl očekávat od 1.19 krát velkého, 15.5 palcového mono-zrcadla. Proto jsem začal uvažovat o tom, jak bych se mohl přiblížit tomuto srovnání bino-dalekohledu přímo s větším dalekohledem, který nese větší, jediné zrcadlo.
Závěry
Vědecký výzkum o významnosti a hodnotě binokulárního součtového faktoru má dlouhou historii. Z rozsáhlé literatury je zřejmé, že je velmi obtížné přiřadit přesnou a jednotnou hodnotu tomuto faktoru. To nemusí být překvapující vzhledem k tomu, že binokulární pozorování zahrnuje mnoho různých aspektů. Nejen pouze fyzické složky očí, ale také komplexní neurální procesy hrají klíčovou roli v binokulárním pozorování. Jeden jediný binokulární součtový faktor proto pravděpodobně nestačí k pokrytí všech aspektů binokulárního pozorování. Kromě toho existuje ohromující rozmezí v tom, jak mohou různí jednotlivci vnímat aspekty binokulárního pozorování. Proto je třeba věnovat maximální pozornost zevšeobecňování závěrů. Částečné úvahy a jednoduché vzorce pro porovnání dalekohledu (nebo dvou zrcadlových bino-dalekohledů) k jednomu většímu zrcadlu jsou téměř jistě zavádějící v tom nejlepším případě. Toto, zdá se, bude stále neuspokojivým výkladem v amatérské astronomii. Jedna cesta z tohoto problému může být a to přímo srovnávat velký bino-dalekohled s velkým mono-dalekohledem. Přinejmenším pro bodové zdroje světla, tj. hvězdy, lze stanovit limitní magnitudy a z nich vypočítat binokulární součet pro tuto konkrétní situaci. V druhé části článku uvedu takové přímé měření. Rovněž se v něm budu zabývat relevancí faktoru souhrnu binokulárního součtu pro pozorování DSO s porovnáním jiných faktorů, které podporují binokulární pozorování.
Poděkování
Řada lidí komentovala otázky, které jsem jim poslal. Tyto otázky se týkaly binokulárního součtového faktoru a jeho význam pro vizuální pozorování DSO objektů. Chci poděkovat za jejich čas za odepsané odpovědi a sdílení jejich názorů a myšlenek. V abecedním pořadí to jsou Phil Harrington, Bruce Sayre, Gary Seronik a Mark Suchting. Jsem zvláště dlužen Melovi Bartelsovi, Janu Van Gastelovi a Dr. Thomasovi Salmonovi. Byli velmi inspirativní a povzbuzovali mě, abych pokračoval v hledání literatury a jejich komentáře zaostřily obsah tohoto článku. Mel Bartels také navrhl přímé měření limitní magnitudy a dovolil mi citovat jeho výsledky.
Reference
Anderson, P.A., and Movshon, J.A. 1989. Binocular combination of contrast signals. Vision Res.
29:1115-1132.
Campbell, F.W., and Green, D.G. 1965. Monocular versus binocular visual acuity. Nature 208: 191-192.
Frisen, L., and Lindblom, B. 1988. Binocular summation in humans: evidence for a hierarchic model. J Physiol. 402: 773-782.
Harrington, P. 2011. Cosmic Challenges, Cambridge University Pres. p. 5.
Meese, T.S., Georgeson, M.A., and Baker, D.H. 2006. Binocular contrast vision at and above threshold. Journal of Vision 6: 1224-1243.
Nelson-Quigg, J.M., Cello, K., and Johnson, C.A. 2000. Predicting Binocular Visual Field Sensitivity from Monocular Visual Field Results. Invest. Ophthalmol. Vis. Sci. 41: 2212-2221.
Pirenne, M.H. Binocular and Uniocular Threshold of Vision. 1943. Nature 152: 698-699.
Salmon, T. ( http://arapaho.nsuok.edu/~salmonto/vs3_materials/Lecture10.pdf )
Sayre, B. 2012 ( http://www.brucesayre.net/#The_science_of_binocular_vision )
Zarenski, E. on Cloudy Nights.
(http://www.cloudynights.com/ubbarchive/showflat.php/Cat/0/Number/913943/page/0/view/collapsed/sb/5/o/all/fpart/all/vc/)sual.html)
a
http://www.cloudynights.com/ubbarchive/showthreaded.php/Cat/1,2,3,4,5,8,9,10/Number/796456/page/1/view/collapsed/sb/5/o/all/vc/1
Binokulární součtový faktor a jeho význam pro DSO pozorování
Část 2, měření a pozorování
Obecně
Bino-dalekohledy s velkými zrcadly jsou vzácné a amatéři astronomové se zajímají o jejich výhody pro DSO pozorování. Toto často končí jednou otázkou: jak velká jsou dvě zrcadla bino-dalekohledu srovnání s jedním a větším zrcadlem? Teoretická odpověď na tuto otázku je zčásti v závislosti na kvantitativní hodnotě tzv. binokulárního součtového faktoru . V části 1 tohoto článku jsem se zabýval historickými a vědeckými aspekty tohoto faktoru, stejně jako diskuse o jeho kvantitativní hodnotě a významu. Spor je z velké části způsoben úplným nedostatkem solidních údajů. I proto jsme přímo porovnávali 2 x 13 palcový bino-dalekohled s 16 palcovým mono-zrcadlovým dalekohledem za účelem zjištění jejich příslušných limitních magnitud. Zde v druhé části článku popisuji výsledky porovnání. Obecný názor mezi amatérskými astronomy napovídá, že by měly být 2 x 13 palcová zrcadla ekvivalentní jednomu zrcadlu o velikosti 15,5 palce. Zjistil jsem však, že limitní magnituda 2 x 13 palcového bino-dalekohledu je konzistentně vyšší než u 16 palcového zrcadlového dalekohledu. Také u plošně rozsáhlejších objektů, jako jsou galaxie, jsou rozdíly ještě větší ve prospěch bino-dalekohledu. Mluvím tedy o tom, co tato zjištění znamenají pro binokulární součtový faktor. Diskutuji také o faktoru binokulárního součtu v kontextu jiných aspektů binokulárního pozorování a tvrdím, že samotný faktor je pouze sám o sobě limitován relevancí DSO pozorováním.
Úvod
Jak lze srovnávat velký zrcadlový bino-dalekohled s "mono-dalekohledem", který má větší zrcadlo? Tak jak bylo vysvětleno v první části článku, může binokulární součtový faktor a jeho kvantitativní hodnota hrát důležitou roli ve srovnání dvou zrcadel s jedním větším zrcadlem. Vědecká literatura je velmi opatrně přiřazení jedné hodnoty binokulárnímu součtovému faktoru a jeho interpretaci. V amatérské astronomické komunitě převažující názor předkládá Zarenski (2006) na Cloudy Nights a Phil Harrington ve své knize Cosmic Challenges (Harrington, 2011). Přiřazují jednoduchý vzorec srovnání dvou zrcadel ve srovnání s jedním větším. Tento vzorec je √ (A2 x 1.41). Kde, A označuje průměr jedné binokulární čočky (nebo zrcadla bino-dalekohledu). Tím myslím, že člověk musí vynásobit průměr jednoho objektivu/zrcadla bino-dalekohledu faktorem 1.19, abyste získali průměr srovnatelného jediného objektivu/zrcadla. Nicméně pozorovatelé, kteří přímo porovnávali velké bino-dalekohledy se srovnatelnými zrcadly tvrdí, že jejich dojem je, že tento faktor je příliš nízký.
Jedním ze způsobů, jak řešit tento spor, je přímo porovnat velký bino-dalekohled s velkým mono-dalekohledem. Alespoň pro bodové světelné zdroje, tj. pro hvězdy, lze určit limitní magnitudu a z toho vypočítat binokulární součtový faktor pro danou konkrétní situaci. Zde představuji takové přímé měření. Nakonec se také zabývám relevancí faktoru sumarizace binokulárního DSO pozorování, ve srovnání s jinými faktory, které upřednostňují binokulární pozorování.
Měření limitních veličin bino-dalekohledu a srovnatelného zrcadlového teleskopu
Takže otázka zní: jak velikost dvou zrcadel porovnat s jedním větším zrcadlem? Jedna cesta, jak toto testovat, je určení limitních magnitud hvězd za stejných podmínek pozorování a porovnat je jak pro bino-dalekohled, tak pro srovnatelně větší zrcadlový dalekohled. Určíme limitní magnitudu jednoduše na nejslabší hvězdě, kterou lze stále vidět v bino-dalekohledu a v porovnávaném větším zrcadle. Výsledné rozdíly v limitní magnitudy jsou nepřímo změřené hodnoty binokulárního součtového faktoru. Při výměně emailů s Mel Bartels, mi navrhl, abych přímo porovnal bino-dalekohled a ekvivalentní mono-zrcadlový dalekohled Dobson, pro určení limitních magnitud každého dalekohledu. Následoval jsem jeho návrh a porovnal 2 x 13 palců bino-dalekohled s 16 palcovým mono-Dobson dalekohledem v limitních magnitudách (viz obr. 1). Zrcadla 2 x 13 palcového bino-dalekohledu jsou f / 51.0. což je ohnisková délka 1650 mm. 16-palcové zrcadlo je f/4,5, ale používám koma korektor Paracorr, který se mění zrcadlo na f/5.2 a efektivní ohnisková vzdálenost 2080 mm. Při použití stejných okulárů a podobných relativních otvorů f/5 a f/5.2 poskytují výstupní pupily, které se navzájem podobají. Tak například při použití okulárů Ethos o ohnisku 10 mm je výstupní pupila s bino-dalekohledem 10/5 = 2, zatímco výstupní pupila s 16 palcovým dalekohledem je 10 / 5.2 = 1. 92. Tyto výstupní pupily jsou téměř stejné. Toto je důležité, protože při pozorování bodových světelných zdrojů, jako jsou hvězdy, určuje výstupní pupila stupeň „temnosti“ pozadí oblohy. Shoda tmavosti pozadí v každém dalekohledu je tedy více víceméně stejná, což umožňuje správné srovnání. Pouze zvětšení se v každém dalekohledu bude lišit vzhledem k rozdílné ohniskové vzdálenosti.
Ve dvou nocích jsem stanovil limitující hodnotu každého dalekohledu. První noc měla téměř dokonalé podmínky, s SQM blížícím se 22.0 (okem limitní magnituda 7.0) a velmi vysoká úroveň průzračnosti oblohy. Vybral jsem pole hvězd blízko Polárky. Druhá noční podmínky byla poněkud slabší, s hodnotou SQM 21.5 (okem limitní magnituda pouhých 6.6). Průzračnost oblohy byla dobrá. Vybrala dvě hvězdná pole, obklopující NGC 7448 a NGC 7678 v Pegasu.


Obrázek 1. Na levé straně můj 16 "f / 4.5 mono-Dobson dalekohled a vpravo 2 x 13 palce f / 5.0 bino-dalekohled.
Další obrázky těchto nástrojů naleznete na svých webových stránkách ( http://arieotte-binoscopes.nl/Binoscopes.htm )
Výsledky jsou uvedeny v tabulce 1. Limitní magnitudy byly určeny na příslušném poli hvězd s 2 x 13 palcovým bino-dalekohledem (sloupec 2 x 13) a 16-palcový mono-zrcadlovým Dobson dalekohled (sloupec 16). Jak lze očekávat, limitní magnitudy z druhého pozorování jsou poněkud nižší než během první noci, kvůli nižší temnotě oblohy. Také s menším pupilou
(vyšší temnota pozadí oblohy) se zdá, že rozdíly budou o něco větší.
Hlavním závěrem však je, že když jsou brány jako celek, limitní magnitudy bino-dalekohledu jsou konzistentně vyšší, než u jediného zrcadlového 16 palcového dalekohledu. To není kompatibilní s převládajícím názorem, že 2 x 13 palcový bino-dalekohled by se měl chovat jako jeden 13 x 1.19 = 15.5 palcový dalekohled.
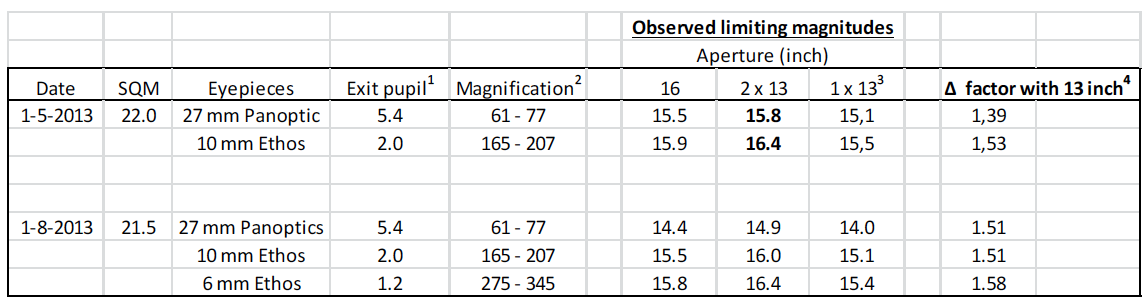
1. Vypočítáno pro bino-dalekohled f/5.0. S Paracorrem je dalekohled o průměru 16 palců f/4.5 má relativní otvor f/5.2 výstupní pupily jsou tímto korigovány.
2. První zvětšení je pro bino-dalekohled 2 x 13 palců, druhé zvětšení je pro dalekohled 16 palců s Paracorrem.
3. Pro výpočet limitní magnitudy pro jedno zrcadlo o velikosti 13 palců, ve srovnání s 16 palcovým zrcadlem, se používá se následující vzorec: M-5 * log (průměr 400 / průměr 330). Například pro 10 mm Ethos dne 1.5.2013: 15.9 - 5 * log (400/330) = 15.9 - 5 * 0.08354 = 15.9 - 0.417 = 15,48 (15.5 je zaokrouhleno!)
4. Pro výpočet nárůstu dvou 13 palcových zrcadel ve srovnání s jedním zrcadlem o průměru 13 palců je použit následující vzorec: 10 ^ (1/5 * (Mag_bino-Mag_mono)). Například pro 10 mm Ethos dne 1.5.2013: 10 ^ 1/5 * (16.4 – 15.48) = 10 ^ 0.184 = 1.53.
Tabulka 1. Výsledky, které zobrazují limitní magnitudy při použití 2 x 13 palcového bino-dalekohledu nebo 16 palcového Dobsona. Přečtěte si text pro vysvětlení.
Pozorování jiných pozorovatelů
Během stejného období Mel Bartels a někteří zkušení pozorovatelé srovnávali 2 x 8 palců bino-dalekohled s 12 nebo 13 palcovým mono-zrcadlovým Dobsonem. Rozdíl v srovnatelných průměrech mezi 2 x 8 palce a 12 nebo 13 palcovými mono-zrcadly činí 1.5 až 1.62. Dospěli k závěru, že z hlediska limitních magnitud byl bino-dalekohled "jen o malinko hůře“ než větší mono-zrcadlové dalekohledy (Mel Bartels, z osobní komunikace). Kombinací jejich dat s mými, se dá bezpečné konstatovat, že zvětšení průměru o 1.4 až 1.5 x je více než dříve deklarovaný nárůst o 1.19 x, což by vedlo k předpokládanému průměru zrcadla 9.5 palce.
Zatímco výše uvedené se týká pouze bodových světelných zdrojů, jiný obraz poskytují plošné objekty, jako jsou mlhoviny a galaxie. Problémem je, že rozdíly na plošných objektech je o hodně těžší přesně kvantifikovat. Nicméně, Mel Bartels dále říká, že "ale mlhoviny byly stejné nebo lépe viditelné v hrubých detailech a * každý pozorovatel * souhlasil, že je esteticky 8 " bino-dalekohled lepší na plošných objektech "(Mel Bartels, z osobní komunikace). Nejčastěji byla citována kvantitativní hodnota spojená s nárůstem ekvivalentního průměru při plošných objektech 1.7 x.
V roce 2014 Oregon Star Party Telescope Walkabout, Jerry Oltion to prokázal ve svém 2 x 12.5 palcovém během tří pozorovacích nocí. ( http://www.bbstrodesigns.com/osp14/osp14.html#Jerry_Oltion ). "Bino efekt se ukázal s výrazným ziskem magnitudy, obvykle na všech objektech a hvězdách a co víc, galaktický cluster Hickson 84, kde bino-dalekohled ukazoval slabší galaxie než 17 magnitudy, kde jedno 12.5 palcové zrcadlo dosáhnulo 16th magnitudy”. (to je zvýšení o 10^1/5*(17 - 16) = 10^0.2 =
1.58 (moje kalkulace)). Pozorovatelé uváděli, že "výkon je podobný jako v 18 palcovém zrcadlu a až v 24 palcovém dalekohledu, v závislosti na objektu ". To je faktor 1.44 až 1.9 x rozdíl v průměru! To je v souladu s tím, co jsem popsal v tomto článku. Navíc "mlhovina Činka byla docela úchvatná - jedna z nejlepších objektů v dalekohledu ". Nebo "jeden objekt, který vynikal lépe v Jerryho bino-dalekohledu, než v jakýkoli jiném dalekohledu, bez ohledu na velikost, byla M31, galaxie Andromeda. Tmavé prachové pásy byly velmi nápadné ".
Také Peter Vercauteren prohlásil, že: Po více než ročním používání mého 18" bino-Dobsonu, kdy jsme jej porovnávali s jinými dalekohledy, včetně 27" mono-Dobsona, mohu potvrdit, že a 18 "bino je přinejmenším rovno, ne-li lepší než 25" mono Dobson. Na slabých objektech jsem dokonce dokázal rozlišovat více podrobností než v 27"mono Dobsonu. (https://www.cloudynights.com/topic/588506-binoquadroculars/page-2).
Já sám dokážu potvrdit, že plošné objekty těží z binokulárního pohledu. Například s 20-palcovým dalekohledem jsem pravděpodobně viděl M51 jako trochu jasnější. Ale s 2 x 13 palcovým bino-dalekohledem vidím mnohem více detailů a kontrastu v ramenech a okolí M51 než u 20ti palce. Toto pozorování není jediná moje zkušenost. Podobně jsem viděl bino-dalekohledem velmi slabé ramena M81, mnohem víc prokreslená a rozložitější, než s 20ti palcem. A jsou ještě dramatičtější pohledy na M31, mlhovinu Andromeda. Extrémně velké a slabé haló je snadno viditelné v obou 2x 13 palců bino-dalekohledu i v 20ti palci. Ale s bino-dalekohledem je vidět ostrý přechod mezi středem a okrajem okolí galaxie a prostor za ním. Jinými slovy, s bino-dalekohledem vidíme lépe, kde končí okraj galaxie M31. To lze snadno vypozorovat, když člověk pomalu přejíždí očima kolem okraje galaxie. Taková pozorování jsou důsledkem rapidně zvýšeného kontrastu, který lze získat díky bino-dalekohledu.
Níže na obrázku 2 ukazuji, jak jsem pozoroval mlhovinu M27 pomocí buď 20 "f / 4.0 mono-dalekohledu a 2 x 13" bino-dalekohledu. To, co vyniká, není ani tak celkový jas, ale velmi vysoký kontrast v detailech, jako jsou vláknité struktury.
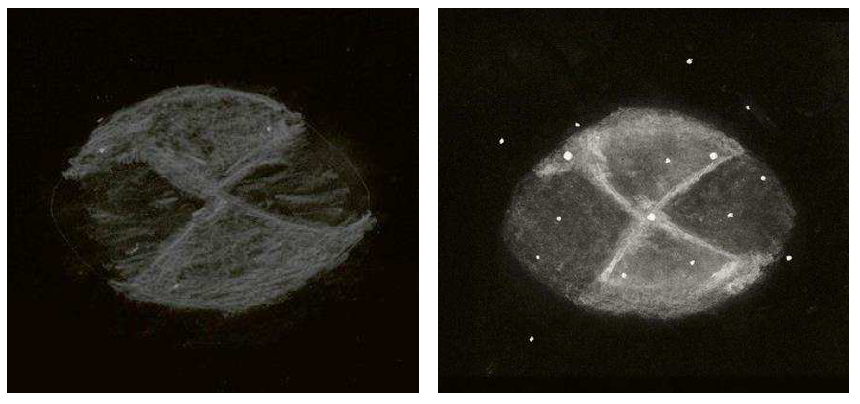

Obr. 2. Vlevo náčrt mlhoviny M27 s 20ti palcovým f/4 mono-Dobsonem a pravý náčrt mlhoviny činky pozorovaný přes 2 x 13 palce f/5.0 bino-dalekohled.
Ačkoli většinou kvalitativní povahy, všechny tyto pozorování směřují stejným směrem. Na plošné objekty jsou dvě zrcadla v bino-dalekohledu přinejmenším srovnatelná s 1.4 až 1.5 větším průměrem mono-zrcadla. To je výrazně lepší než předpokládané zvýšení průměru o 1.19.
Co tyto poznatky přináší pro binokulární součtový faktor a jeho použití?
Kde tedy končí hodnota, pokud jde o binokulární součtový faktor a jeho význam? V převládající interpretaci by se průměr jednoho zrcadla měl zvětšit o faktor 1.19. To vychází ze vzorce √ (A2x1.41) = A x 1.19, ve kterém by byl binokulární součtový faktor 1.41. Výše citované pozorování však vyžadují zvýšení průměru faktorem v rozmezí 1.4 až 1.4. Pro konkrétní užití tohoto vzorce by znamenalo používat binokulární součtový faktor mezi 2 až 2.9. Tak jak bylo vysvětleno v prvním článku, je hodnota 1.41 pro součtový faktor spíše obecná a byly evidovány hodnoty mezi 1,1 a 2. Nicméně hodnota 2.9 se zdá být vysoká a nepravděpodobná.
Zdá se pravděpodobnější, že poměrně zjednodušující použití binokulárního součtového faktoru a jeho využití předpovídat větší, srovnatelné mono zrcadlo není platné. Jak je uvedeno v prvním článku, všechny výzkumy týkající se součinitele souhrnu binokulárního součtu zahrnuje srovnání mezi levým a pravým oko a kombinaci obou očí. Levé a pravé oko mohou být víceméně srovnatelné nebo jedno z nich může mít vadu, ale nikdy nejsou porovnávány dvě oči s jediným VĚTŠÍM okem. To je nemožné a proto neexistuje žádný vědecký výzkum, který by tento problém řešil z tohoto úhlu pohledu.
Přesto se toho snaží amatérští astronomové dosáhnout. Takže přestože ne všechny pozorování výše musí být platné, tak vzorec √ (A2x1.41) nemůže být správný. To zanechává také otázku kvantitativní hodnoty binokulárního součtového faktoru v tomto specifickém kontextu široce otevřenou.
Binokulární součtový faktor ve srovnání s jinými faktory, které podporují binokulární pozorování
Za předpokladu, že by činitel binokulárního součtu dosáhl poměrně vysoké hodnoty 2, jaká má jeho hodnota skutečný dopad na DSO pozorování? Tato hodnota by v často citovaném vzorci vyústila na hodnotu přibližně ekvivalentu zdvojení průměru zrcadla. Takže by 2 x 13 palcový bino-dalekohled odpovídal 18.2 palcovému mono-zrcadlu. Jak je znázorněno na obrázku 4, toto zdvojnásobení v oblasti shromažďování světla zrcadly by přineslo v průměru zvýšenou limitní magnitudu o ~ 0.7 (Bartels, 2012). Chcete-li dát toto číslo do správné perspektivy: když jsem v mém rodném městě, dosáhnul limitující magnitudy 4.7, tak jsem měl štěstí. Na francouzském venkově je snadno dosažitelná hraniční hodnota 6,7. Zisk jsou 2 plné magnitudy a trpasličí hodnota 0.7 x zvýšení v limitní magnitudě, které lze dosáhnout změnou z ekvivalentního zrcadlového mono-dalekohledu na bino-dalekohled. Jestliže by byl binokulární součtový faktor v shromažďování více světla jediným argumentem pro bino-dalekohled, rád bych dodal: "Neobtěžujte se tím".
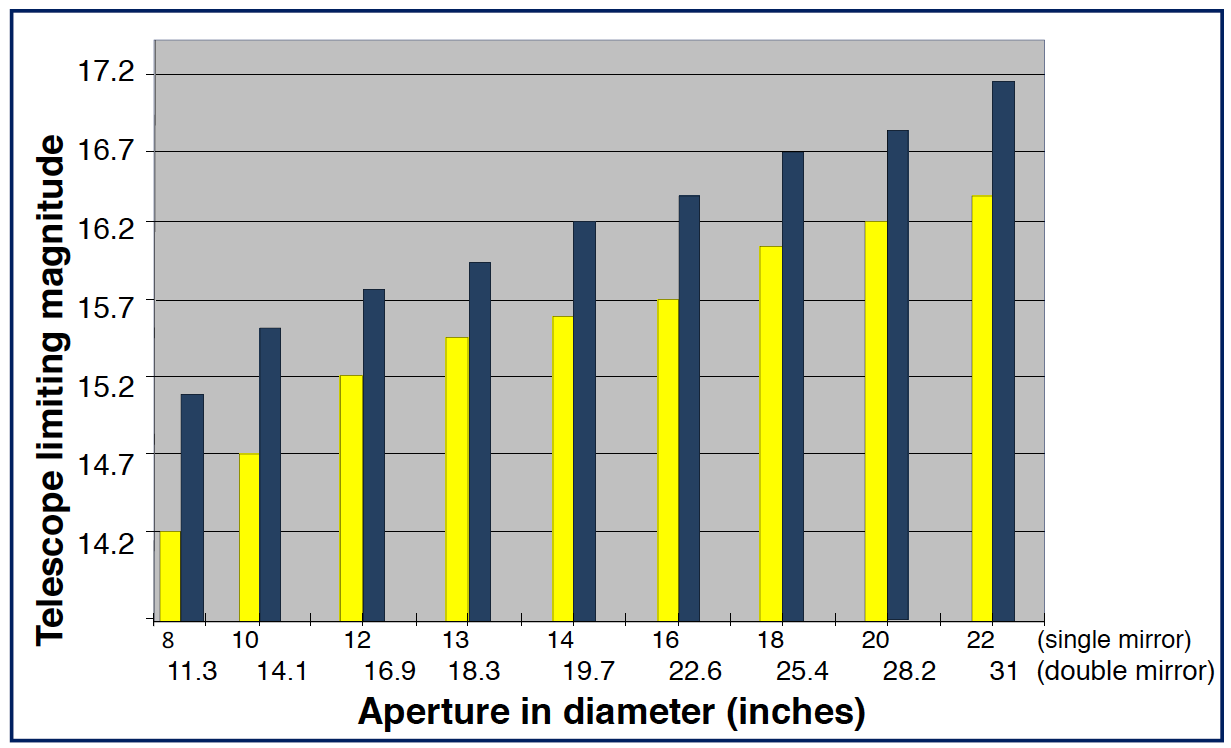
Obrázek 3. Mezní magnitudy, které odpovídají různým průměrům zrcadel. Žlutě jsou průměry v palcích a průměr je uveden v horním řádku čísel (single mirror). Modře jsou zdvojené průměry (dvojnásobné plochy), (přepočtené vzorcem √ (A2 x 2) – pozn. překladatele) na průměr jednoho zrcadla (double mirror), označené spodním řádkem čísel. Všimněte si, že rozdíl mezi žlutým a modrým sloupce je trvale ~ 0.7 magnitudy. Také nárůst z 12 palců na 16 palců (přibližně zdvojnásobení plochy) vede k nárůstu o 0.7 v limitní magnitudě. Čísla jsou odvozena od Mela Bartelse. (Bartels, 2012).
Co by pak bylo hlavními faktory, které určují přínosy bino-dalekohledu po plošných objektech oproti mono-dalekohledu?
1. Nejdůležitějším faktorem je lepší poměr signálu k šumu, který vede k vnímání tmavšího pozadí oblohy. Jedná se o jediný nejdůležitější faktor, který upřednostňuje bino-dalekohled ve srovnání s velkým mono-zrcadlovým dalekohledem. Tento výsledek se projeví jako rozdíl v lepším kontrastu bino-dalekohledu oproti velkému jedinému zrcadlovému dalekohledu. Co to znamená? Podnět, který nepochází z astronomického objektu (například "světelný šum" ze světelného znečištění) může být interpretováno jedním okem jako správný a použitelný signál. Ale šance, že tyto náhodné světelné signály zasáhnou obě oči současně a spojí se v mozku je opravdu velmi malý. Jinými slovy, při pohledu oběma očima musí mozek potlačit mnohem menší šum pozadí vytvořený světelným znečištěním. A to se automaticky překládá jako ztmavení pozadí oblohy, dokonce i v mém světelně znečištěném rodném městě. Výsledný zlepšený kontrast je zvláště významný pro pozorování velmi slabých objektů jako galaktické haló nebo ramena. V rámci těchto slabých, plošných objektů je mnohem více viditelných podrobností a je zvýšen kontrast uvnitř objektů. Za tento jev je pravděpodobně zodpovědný neurální součet. Bino-dalekohled má také výraznou výhodu nad binohlavou, která jednoduše rozdělí JEDEN světelný signál na dva. S binohlavou se redukce signálu náhodného šumu se nemůže v zásadě uskutečnit! (rovněž nelze uskutečnit redukci různého seeingu, jak tomu je ve dvou tubusech – pozn. překladatele)
2. Stereopozorování je schopnost vidět prostorovou hloubku. Díky rozdílným umístěním očí je objekt viděný každým okem z trochu jiného úhlu (paralaxa). To vytváří prostorový 3D efekt. Čím je objekt blíže, tím větší je úhel a větší je 3D efekt. Bohužel astronomické objekty jsou tak vzdálené, že tam neexistuje žádná taková věc jako paralaxa a tedy žádné "skutečné" stereopozorování. Existuje však související jev nazvaný chromatické stereopozorování nebo chromostereopsie. To je způsobeno například mírně odlišnou aberací očních čoček v červeném a modrém světle. V důsledku toho se červené a modré světlo zaostří na poněkud odlišném místě sítnice. Tento efekt je pro každé oko odlišný, a proto se zdá, jako by červené hvězdy byly trochu blíže než modré hvězdy. Při pozorování bino-dalekohledem se vytváří chromostereopsie iluze prostorové hloubky, i když je to zcela umělé.
3. Pocit širšího zorné pole, které lze dosáhnout bino-dalekohledem, lze těžko dosáhnout s velkým mono-teleskopem, tedy věc, kterou často zdůrazňuje Mel Bartels. Opravdu, pokud se díváte přes bino-dalekohled, je tento krásný efekt okamžitě zřejmý. Ale proč je tomu tak? Vezměme si jako příklad můj 2 x 13 palcového bino-dalekohled s f/51.0 zrcadly, použijme dva 10 mm Televue Ethos, které poskytují 165 x zvětšení a FOV 0.61 stupně. Předpokládejme, že má tento bino-dalekohled přibližný ekvivalent 18-palcového mono-dalekohledu, který je také f/5.0. Nyní 10 mm Ethos poskytne zvětšení 225 x a FOV 0.45 stupně, což je o polovinu méně FOV jež vidíte s bino-dalekohledem. Chcete-li dosáhnout 165 x zvětšení a 0.61 stupně pravého pole, 18 " musí být f/3.7. A protože tím vznikne masivní koma, bude zapotřebí Paracorr, který komu sníží. Jeho důsledkem musí být zrcadlo dokonce f/3.2 pro stejné zvětšení a FOV (Televue Eyepiece Calculator!). Nyní zvažte, jaké budou náklady na tak světelné zrcadlo!
Je zde další aspekt, který je zřídka řešen. Lidé mají horizontální binokulární vizuální pole 120 stupňů. Ale je zde je další monokulární pole o 45 stupních na obou stranách binokulárního pole. Takže je zde celkem 90 stupňové pole, které není binokulární, ale je vnímáno dvěma očima. Při pohledu pouze jedním okem je to jen pouhých 45 stupňů jednoho oka. A i když nemůžete zahrnout celou 120 stupňů plus 90 stupňů na jednoho pohledu, uvidíte to periferně a to zvýší pocit „ponoření do obrazu“. Samozřejmě, že je důležitý výběr okulárů např.: se dvěma 50 stupňovými okuláry, uvidíte, že pole je omezené. Účinky jsou ovšem zřejmé, když se použijí dva okuláry 100 stupňové Ethos s velkým zorným polem.
4. Dokonalý komfort pozorování se dvěma očima. Existuje také "obyčejný" efekt zlepšeného komfortu při pohledu dvěma očima namísto jedním okem a druhým okem zavřeným. Trvalé soustředěné pozorování slabých detailů se dvěma očima, aniž by to bylo přínosnější, než jedním okem, je příjemnější a relaxační.
5. Zisk v limitní magnitudě nebo zisk v průměru, který činí bino-dalekohled srovnatelný s větším mono-dalekohledem. To je téma tohoto článku. Bohužel, jak bylo vysvětleno, tento aspekt dostává nejvíce pozornosti.
Závěr
Použitím specifické hodnoty binokulárního součtového faktoru k možné předpovědi, jak velký průměr dvou zrcadel v bino-dalekohledu srovnávat s jedním, větším zrcadlem, je způsob přinejmenším zavádějící. Za prvé se značně liší experimentálně určené hodnoty binokulárního součtového faktoru a ty ovlivňují teoretické předpovědi. Za druhé, vědecké experimenty, které zkoumají jevy pozorování, jako je faktor binokulárního součtu, jsou založeny na použití jediného levého nebo pravého oka versus použití dvou očí a nejsou zvyklé předpovídat, jak velké jedno jediný, větší „Cyklop“ oko bude ve srovnání s našima dvěma očima. To je však přesně to, o co amatérští astronomové usilují, že je dovedou k vytouženým výsledkům.
Přímé srovnání mezi velkými bino-dalekohledy a většími, mono-zrcadlovými dalekohledy naznačují, že nárůst velikosti většího srovnatelného zrcadla se pohybuje mezi faktory 1.4 až 1.7. Toto je pravděpodobnější než běžně používaný vzore √ (A2 x1.41), který předpovídá zisk 1.19 x v průměru většího zrcadla. Buď jsou tato pozorování špatná, nebo je špatné použití tohoto vzorce a jeho předpovědí. Mám sklon věřit tomu poslednímu.
Dalším argumentem je, bez ohledu na jeho kvantitativní hodnotu, že má binokulární součtový faktor jen omezenou relevanci pro DSO pozorování. Zvýšený poměr signálu k šumu, který je dosažen bino-dalekohledem, je pravděpodobně nejdůležitější pro příznivé účinky při pohledu dvěma očima přes bino-dalekohled. Nicméně tvrzení o skromném zlepšení 1.19 x obrazu v bino-dalekohledu (nebo binokuláru), pokud jde o zisk světla, i tak pravděpodobně přináší mnoho potenciálních uživatelů/stavitelů bino-dalekohledů. To je politování hodné, mírně řečeno.
Poděkování
Mnoho lidí komentovalo otázky, které jsem jim poslal. Tyto otázky se týkaly součtového faktoru a jeho významu pro vizuální pozorování DSO objektů. Chci jim poděkovat za jejich čas, že mi napsali a sdíleli své názory se mnou. V abecedním pořadí jsou to Phil Harrington, Bruce Sayre, Gary Seronik a Mark Suchting. Zvláště pak děkuji Mel Bartels, Jan van Gastel a Dr. Thomas Salmon. Byli mi velice přínosní a povzbuzovali mě, abych pokračoval v hledání literatury a jejich komentáře nakonec vytvořily obsah tohoto článku. Mel Bartels také navrhl, abych přímo měřil limitní magnitudy a nechal mě citovat jeho výsledky.
Odkazy
Bartels, M. 2012. Visual astronomy. (http://www.bbstrodesigns.com/visual.html).
Campbell, F. W. a Green, D.G. 1965. Monocular versus binocular visual acuity. Nature 208: 191-192.
Harrington, P. 2011. Cosmic Challenges, Cambridge University Pres. str. 5.
Pirenne, M.H. Binocular and Uniocular Threshold of Vision. 1943. Nature 152: 698-699.
Zarenski, E. na Cloudy Nights.
(http://www.cloudynights.com/ubbarchive/showflat.php/Cat/0/Number/913943/page/0/view/collapsed/s b/5/o/all/fpart/all/vc/)sual.html)
a
http://www.cloudynights.com/ubbarchive/showthreaded.php/Cat/1,2,3,4,5,8,9,10/Number/796456 /page/1/view/collapsed/sb/5/o/all/vc/1


