Potřeba testovat kvalitu optických přístrojů je stejně stará jako optické přístroje sami. Z počátečních přístupů typu pokus-omyl postupně přinesl pokrok v polovině 18. století R. Smith a zejména pak Herchel se svým testování zonálních vad prostřednictvím masek. Skutečnou revoluci pak přinesl až v polovině 19. století L. Foucault se svým stejnojmenným testem. I přes nesporné výhody Foucaultova testu však stále chyběla metoda, která by umožňovala určit kvalitu optického systému rychle byť jen orientačně. V roce 1922 byl Vasco Ronchim publikován postup testování optických zrcadel velkých průměrů pomocí mřížek. Mnohem později byl tento test nazván po svém autorovi – Ronchiho test. Od svého prvního publikování doznal tento test mnoha variací a díky své jednoduchosti se stal zejména mezi astronomy amatéry velmi populární.
Základ Ronchiho testu
Základní realizace Ronchiho testu je poměrně jednoduchá. Mějme testovaný objektiv (např. zrcadlo). Umístíme-li do okolí dvojnásobku ohniskové vzdálenosti zdroj (pro jednoduchost nyní uvažujme pouze bodový). Objektiv promítne obraz bodu do příslušné vzdálenosti dané zobrazovací rovnicí. Za/před tento obraz zdroje nyní umístíme testovací mřížku. Pozorujeme-li nyní přes tuto mřížku testovaný objektiv (zrcadlo), uvidíme na jeho povrchu soustavu světlých a tmavých pruhů, tzv. Ronchigram. Při posouvání testu směrem k rovině, ve které je formován obrazu bodu (tzv. obrazová rovina), se budou pozorované pruhy roztahovat. Tzn. jejich počet se bude zmenšovat a poroste jejich tloušťka. V okamžiku, kdy bude mřížka v obrazové rovině lze pozorovat obraz obdobný Foucaltovu testu. Při pohybu směrem od obrazové roviny se budou pozorované pruhy „nahušťovat“ (tj. poroste jejich pozorovaný počet). Z průběhu a tvaru pozorovaných pruhů lze přitom usuzovat na kvalitu optické soustavy.
Příklad jednoduché realizace Ronchiho testu je na obrázku 1. Světelný tok ze zdroje za pomocí polopropustného zrcadla prochází přes mřížku na testovanou optickou soustavu - např. zrcadlo. Od něj se odráží svazek zpět k pozorovateli. Ten vracející se svazek pozoruje přes mřížku. Z uvedeného je patrné, že každý Ronchiho test je složen z několika nezbytných části.
Osvětlení v Ronchiho testu se skládá z vlastního zdroje světla, difuzéru a prostorového filtru.
Na vlastní zdroj světla nejsou kladeny žádné zásadní požadavky. Světelný zdroj nemusí být přísně monochromatický (např. laser). V případě testování soustav s disperzními materiály (refraktory) zpravidla plně postačí prostý barevný filtr, popř. vhodné následné zpracování. Je-li Ronchiho test vyhodnocován vizuálně, musí mít i přiměřený světelný výkon. Tzn. zejména maximální, aby nehrozilo riziko poškození zraku. Raději proto v tomto případě rovnou zapomeňte laserové moduly s výkonem přes 1mW. Pro fotografický záznam je větší světelný výkon zdroje samozřejmě přípustný (a mnohdy dokonce nutný). Pro běžné testování není zpravidla použití laserů nutné. Pro jednoduchý tester funkci světelného zdroje velmi dobře zastane i obyčejná žárovička či LED dioda. Pokud přeci jen máte v úmyslu využít monochromatického zdroje (např. zdroj bude určen i k jiným druhům testů) zpravidla postačí laser s výkonem pod 1mW (tedy oku relativně bezpečný). Tomuto účelu vyhovuje i upravené laserové ukazovátko. Vlastní úprava je velmi prostá – postačuje vyšroubovat kolimační čočku, která je umístěna ve vlastním těle ukazovátka pod nástavci s hologramy (zpravidla výměnnými). Vlastní laserová dioda je velmi malá a tak obdržíme poměrně slušný bodový zdroj. Na místo kolimační čočky pak stačí našroubovat dirkovou clonu (např. plynovou trysku), která bude plnit funkci prostorového filtru.
Ve funkci světelného zdroje lze využít i vzdálených zdrojů s vlastním prostorovým filtrem v potřebné vzdálenosti od testovaného objektivu. Vzdáleným zdrojem může např. být i diaprojektor či hvězda na obloze (v tomto případě platí určitá specifika).
Účelem difuzéru je homogenizovat (zrovnoměrnit) světelný tok ze zdroje, který bude procházet prostorovým filtrem. Je-li světelný tok dostatečně rovnoměrný, lze jej vynechat.
Prostorový filtr moduluje vystupující světelný svazek. V závislosti na typu testu se využívá:
1. Dirková clona (bodový zdroj) tvořená velmi malým kruhovým otvorem. Tento typ modulátoru lze využít prakticky pro všechny typy Ronchiho testů. Zdroj lze tedy využít u nelineárních testů, které s jinými typy zdrojů nefungují (např. Mobsbyho test). Výsledky pomocí dirkové clonky jsou nejzřetelnější. Proto ji lze doporučit zejména pro začátečníky. Nevýhodou je mnohem menší množství světla, které je k měření k dispozici (pro tyto účely se mi osvědčily právě upravená laserová ukazovátka). Další nevýhodou jsou zvýšené nároky na kvalitu pozorovací mřížky.
2. Štěrbina poskytuje mnohem více světla než předchozí případ. Je vhodná i v případě méně kvalitních mřížek.
3. Modulační mřížka. Máme-li dvě mřížky (popř. jednu dostatečně velkou pro zdroj i pozorování), lze ji využít ve funkci prostorového filtru (jde vlastně o x štěrbin vedle sebe). Pro jednoduchost konstrukce zdroje s využitím jediné mřížky je tato konstrukce velmi používaná.
Testovací mřížka je v nejjednodušším případě tvořena soustavou čar shodné tloušťky i odstupu (lineární test). Existují i varianty testu, kde jsou rovné čáry nahrazeny soustřednými kruhy či křivkami (viz dále).
Minimální doporučená hustota testu jsou 4 páry čar/mm. S rostoucí hustotou testu roste i citlivost testu. Na druhou stranu vyšší hustota testu vyžaduje umístění testu blíže ohnisku a jemnější posuny. Použití extrémně hustých testů je tedy rovněž kontraproduktivní. Doporučené maximum pro běžné použití pro orientační testy je cca 15-20 párů čar/mm.
Pro přesnost je ale nutné uvést, že citlivost a „výkon“ mřížky nelze oddělovat od použitého zdroje. Existují 3 základní varianty kombinací zdroje a mřížky:
1. Mřížkový zdroj (plošný zdroj před který je umístěná lineární mřížka) a „pozorovací“ mřížka.
2. Štěrbinový zdroj a „pozorovací“ mřížka.
3. Bodový zdroj a „pozorovací“mřížka.
Je nutné opět zdůraznit že ne všechny typy mřížek lze použít se všemi typy zdrojů (viz výše).
Varianty uspořádání Ronchiho testu
Ronchiho test lze aplikovat v několika základních uspořádáních:
1. Zdroj i testovací mřížka v blízkosti vrcholu křivosti (dvojnásobku ohniskové vzdálenosti)
2. Zdroj v nekonečnu a testovací mřížka v ohniskové rovině
3. Zdroj i testovací mřížka v ohniskové rovině (autokolimační uspořádání)
Případ, kdy je zdroj i testovací mřížka v okolí dvojnásobku ohniskové vzdálenosti je uspořádání vhodné zejména laboratorní měření. V tomto uspořádání lze využít jakékoliv výše uvedené kombinace zdroje a testovací mřížky. Určitou nevýhodou je větší potřebná délka (prostor) pro testování.
Druhé často využívané uspořádání je situace, kdy je zdroj v nekonečnu. V tomto případě je zdrojem zpravidla hvězda (ať umělá či skutečná). V ohniskové rovině objektivu je pak umístěna mřížka. V tomto případě je mřížka zpravidla lineární. V určitých speciálních případech lze ale využít i některých nelineárních testů (např. Terebitzhův kruhový test). Obrovská výhoda tohoto uspořádání je v možnosti využít objektiv v jeho původním uchycení (tubusu) bez nutnosti jeho demontáže. Mřížku pak lze snadno vložit do okulárového výtahu. Pro snadnost aplikace je právě toto uspořádání mezi astronomy amatéry velmi oblíbené.
Předchozí uspořádání lze využít pro testování prakticky jakékoliv dalekohledové soustavy. Určitým omezením ale je, že ji lze využít zpravidla pouze za tmy (zdrojem je zpravidla jasná hvězda). Navíc v tomto případě může rušivě působit i turbulence atmosféry.
Pro testování menších průměrů refraktorů je možné využít i autokolimačního uspořádání. Zdroj je umístěn v ohniskové rovině objektivu. Ten jej promítá do nekonečna. Před objektivem je umístěno rovinné zrcadlo, které odráží z objektivu vystupující rovnoběžný svazek zpět. Svazek je pak objektivem soustředěn zpět do ohniskové roviny. Zdroj i pozorovací mřížka se tedy v tomto případě nachází v jedné rovině.
Vyhodnocení Ronchiho testu
Orientační vyhodnocení
Kresba mřížky (resp. jednotlivé pozorované pásy) odráží průběh vlastní optické plochy zrcadla. Pozice každého pozorovaného pásu je dána rozhraním mezi světlým a tmavým pásem. Je určitě lákavé za pomocí Ronchigramu ze známých parametrů testu určovat exaktně kvalitu optické soustavy, popř. i poloměry křivosti jednotlivých zón asférických objektivů. Pro první přiblížení je ale nutné se nejprve naučit správně interpretovat výsledky testu. To se neobejde bez zapamatování základních průběhů, které jsou typické pro jednotlivé aberace.
Pro přibližný odhad kvality soustavy není nutné měřit přesnou pozici mřížky od aktuální obrazové roviny. Na základní vlastnosti testované optiky tak lze usuzovat přímo ze vzhledu pozorovaného obrazu (Ronchigramu). Interpretaci Ronchigramu je nutno dělat komplexně. Rozbor dílčích prvků, ze kterých je složen typický Ronchigram je uveden níže.
Teprve pak je možné přistoupit k mnohem detailnější analýze. Pro její vyhodnocení je nutné znát zejména hustotu mřížky (např. 10 párů čar/mm), parametry objektivu (ohniskovou vzdálenost, průměr, …) a pozici testu (před či za ohniskem, velikost ofsetu).
Sférická plocha
Sférické plochy se využívají velmi často u refrakčních optických členů. U zrcadel jsou vhodné pouze u systémů s menším relativním otvorem, popř. u některých katadioptrických systémů.
Pro testování sférických ploch lze použít klasickou čárovou mřížku. Bez ohledu na to, zda je mřížka umístěna před či za ohnisko, pozorovaný obraz bude mít obdobný charakter. V pozorovaném Ronchigramu lze u ideální sférické plochy pozorovat systém světlých a tmavých pásů. Velikost posunu mřížky od ohniska (ofset) se projeví jen změnou počtu těchto pásů. Rovněž není podstatné, zda je počet zobrazených pruhů sudý či lichý, zda je v centru světlý či tmavý pruh, nebo zda jsou pruhy svisle či vodorovně. Výsledek je vždy správný.
Pro nesférické plochy bude průběh poněkud složitější. Obecně je ale možné využít základní lineární test i pro jejich testování. Jen interpretace výsledků je poněkud složitější. V tomto případě je výhodnější pro první intuitivní odhad použít některý z nelineárních testů.
Podívejme se na některé základní průběhy odchylek od sférické plochy a ukažme si, jak se odrazí ve výsledném Ronchigramu. Pro jednoduchost vše demonstrujeme na prostém sférickém zrcadle.
Sféra ve sféře (probroušený střed)
Poměrně často mívají zejména doma vyráběná zrcadla „probroušený“ střed. V tomto případě má vnitřní oblast (zóna) menší poloměr křivosti, než zóna vnější. V tomto případě lze původně celistvou sférickou plochu rozdělit na dvě zóny. Zóna v okolí středu má menší poloměr křivosti (a úměrně s tím i menší ohniskovou vzdálenost) než zóna u okraje.
Předpokládejme mřížku umístěnou za středem křivosti zrcadla (dvojnásobkem ohniskové vzdálenosti). Odpovídající Ronchigram je složen ze dvou oblastí. Pokud jsou obě zóny sférické, jsou čáry v obou rovné a rovnoměrně rozmístěné. Protože vnitřní zóna má menší ohniskovou vzdálenost je pozice mřížky dále od středu křivosti. V tomto případě má vnitřní oblast vyšší hustotu čar (čáry jsou tenčí). Pozorované kruhové zakřivení čar v Ronchigramu odpovídá zobrazení čáry procházející přechodovou oblastí mezi oběmi poloměry křivosti. Takto je poměrně přesně i vymezena vlastní velikost vnitřní zóny.
Pokud je velikost „probroušeného středu“ poměrně malá a mřížka je příliš blízko středu křivosti., nemusí se ve vlastním Ronchigramu její přítomnost projevit. Celá středová oblast může zůstat ukryta uvnitř širokého středového pásu. Proto je doporučený počet zobrazovaných čar právě 3-4 temné pásy.
U soustav s centrálním stíněním je menší „centrální díra“ přípustná bez vlivu na kvalitu optické soustavy (centrální část je stíněna sekundárním zrcadlem). U refrakčních soustav je naopak nepřípustná.
Prstenec
Při dodatečné nedokonalé korekci, popř. pokud je vnitřní zóna z předešlého příkladu je nevhodně odstraněna , zůstane v přechodové oblasti úzký pás tvořící „prstýnek“.
Vlastní Ronchigram je podobný Ronchigramu z předešlého případu. Je zde ale několik odchylek. Čáry procházející okrajem prstýnku tvoří „smyčky“. Mezery (světlý pruh) mezi vnitřním a vnějším regionem jsou identické.
„Srážený“ okraj
Asi nejčastější vadou, se kterou se setkáme u velké části ručně i strojově vyráběných optických prvků, je „sražený“ okraj. Příčinu sražených okrajů je třeba hledat v technologii výroby optických ploch.
Neduhem sražených hran netrpí samozřejmě jen zrcadla, ale i optické prvky využívající zákona lomu (čočky). Na rozdíl od zrcadel jsou ale sražené okraje v tomto případě ukryty v objímkách těchto optických prvků. Proto se na kvalitě zobrazení neprojevují. Pokud chceme omezit vliv i u zrcadel lze k tomu využít drobného triku. Zpravidla stačí zastínit okraj zrcadla clonou s vnitřním průměrem jen o několik milimetrů menší, než je vlastní průměr zrcadla. Vyšší kvalita pozorovaného obrazu za trochu menší optický zisk určitě stojí.
V Ronchigramu se sražené okraje projeví „zalomením“ okrajů čar a jejich nahuštěním při okraji. Pro odhalení „sražených“ okrajů postačí sledovat průběh vybrané čáry. Nejlepší oblast pro ověření je alespoň 1/3 průměru od středové čáry. Nedoporučuje se ale vybírat čáry, které jsou příliš u okraje zrcadla.
Vliv aberací na vzhled Ronchigramu
Doposud byla řeč jen o vlivu deformací plochy zrcadla (resp. výsledné ekvivalentní deformaci u soustav s více plochami) na zobrazený Ronchigram. Mimo dílčích zón s defektem existují samozřejmě i deformace pozvolné, které se projeví pozvolnou změnou Ronchigramu.
Vliv dílčích aberací na vzhled Ronchigramu je demonstrován na souvisejících obrazcích. Jejich projev je pro názornost na připojených obrazcích úmyslně zvětšen. Ve skutečnosti bude jejich projev velmi často mnohem menší a bude se projevovat ve spojení s ostatními vlivy.
Sférická aberace
Klasický Ronchiho test je velmi vhodný na stanovení sférické aberace. Za jeho pomoci je při pečlivé práci odhalitelný tento typ aberace odpovídající deformaci vlnoplochy až o velikosti 1/20. Sférická aberace u kulové plochy způsobuje u lineárního testu „prohnutí“ pozorovaných čar. Míra a směr tohoto prohnutí a jeho směr je přitom závislý na pozici mřížky (před/za ohniskem, velikost posunu od obrazové roviny) a samozřejmě na velikosti sférické aberace. Při testu dostatečně vzdáleném od obrazové roviny můžeme pozorovat test jehož středová oblast je blízká ideálnímu průběhu. Okrajová vykazuje prohnutí. Pro první odhad její velikosti postačuje plynule posouvat test z oblasti za obrazovou rovinou směrem k měřenému objektivu. S klesající vzdáleností od obrazové roviny bude klesat počet čar (stejně jako u ideální plochy). Bude však docházet k jejich postupnému ohýbání.
Přesné určení velikosti sférické aberace z tvaru Ronchigramu je samozřejmě možné. je ovšem již poněkud komplikovanější a náročné na velmi pečlivou práci. Rovněž se již neobejdeme bez měření pozice mřížky od ohniskové roviny. Vlastní velikost aberace dané koeficientem A je dána vztahem:
![]() , (1)
, (1)
kde: A … koeficient sférické aberace,
, … souřadnice středu prohnutí,
d … velikost periody testu,
m … řád odčítaného pruhu (kolikátý pruh je od středního),
T … je dána vztahem ![]()
kde l’ je vzdálenost mřížky od ohniska a r poloměr křivosti vlnoplochy.
Koma
Nesymetrické aberace (koma a astigmatismus) jsou sice obecně Ronchiho testem zjistitelné, vyžadují však obzvláště svědomitou práci. I tak ale mohou v určitých případech zůstat neodhaleny.
Koma se v Ronchigramu projevuje nahuštěním čar do jedné strany. Na straně opačné jsou naopak čáry rozestoupené od sebe a je zpravidla patrné i jejich prohnutí. Pokud pootočíme mřížku zůstává nahuštění ve stejné oblasti pozorovaného objektivu. Vizuálním pozorováním jsme schopni odhalit deformace vlnoplochy vyvolané komou o velikosti tak do 1/10. Pozorovaná velikost bude evidentně záviset na úhlu pozorování, který svírá s optickou osou. Na optické ose bychom přirozeně u slušné optické soustavy neměli zjistit žádnou komu.
Pro číselné vyjádření komy je nutné oproti předešlému případu znát i úhel naklonění , který svírá mřížka s meridiální (poledníkovou) rovinou. Pro hodnotu koeficientu komy B pak platí:
![]() . (2)
. (2)
Astigmatismus
Ronchiho test není podobně jako v případě komy pro stanovení astigmatismu primárně určen. Nejjednodušší metodou jeho zjištění je pravděpodobně pozorování bodového zdroje pomocí okuláru před a za ohniskem (viz. minulý díl seriálu pojednávající o testu na hvězdu). V některých situacích může dokonce Ronchiho testem zůstat astigmatismus neodhalen. Pro jeho zjištění touto metodou je nutné proto občas pootáčet i zrcadlo (popř. mřížku) podél optické osy. Test je nejcitlivější, když svírá s podélnou osou astigmatismu úhel cca 45°. Přesouvejme testovací mřížku směrem k ohniskové rovině. Vliv astigmatismu se projeví natáčením pozorovaných pruhů při přiblížení/průchodu testu ohniskovou rovinou. Z rychlosti přetáčení dokáže zkušený pozorovatel odhadnout i velikost astigmatismu. Pomocí této metody je možné odhalit přítomnost astigmatismu podobně jako v předchozím případě z deformací vlnoplochy do 1/10.
Ke stanovení hodnoty astigmatismu je nutné znát úhel , který svírá pozorovaný obraz pruhu k podélné orientaci mřížky (tzn. k pruhům na mřížce). Přesnost jeho určení není zpravidla příliš vysoká. Proto jeho číselnou hodnotu je nutno brát s určitou rezervou. Obecně pro koeficient astigmatismu C platí:
![]() . (3)
. (3)
Hodnota úhlu se mění se změnou polohy mřížky. Pro poměr T/C mezi -1 až =-3 lze využít zjednodušený tvar, ve kterém není nutné úhel stanovovat. Tento vztah má tvar:
![]() . (4)
. (4)
Nelineární testy
Doposud jsme se zabývali pouze využitím Ronchiho testu pro testování sférických ploch. Ve velké míře se ale dnes setkáváme i s asférickými plochami, zejména parabolickými. Zobrazení klasického lineárního (čárového) testu u ideální asférické (např. parabolické) plochy není pro nezkušeného pozorovatele příliš čitelné. Asférická plocha způsobí zkřivení pozorovaných čar a odhadnout to „správné“ není snadné. Jednoduchý čárový test může být i přesto využit pro testování plynulosti plochy, tzn. k testování přítomnosti lokálních zón. Ty se ve výsledném Ronchigramu projeví lokálním rozšířením/zúžením pozorovaných pruhů, roztřepením jejich okrajů, … .
Pokud chceme rychle orientačně zhodnotit celkovou kvalitu soustavy, je vhodnější využít některý z nelineárních testů. Na rozdíl od prostých čárových se skládají z dopředu napočítaných křivek, které odpovídají testované konfiguraci (excentricitě testované plochy, vzdálenosti testu od ohniska, …).
Nelineárních testů existuje celá řada. Ukažme si alespoň dva snadné na použití i vyhodnocení.
Test asférických ploch Mobsby
Test Mobsby byl původně napočítán pro parabolické plochy. Po úpravách průběhu křivek je jej možno použít obecně pro jakoukoliv plochu. Pro jeho návrh existuje celá řada freeware a shareware programů (např. InvRon, popř. MODAS).
Test předpokládá bodový zdroj umístěný v dvojnásobku ohniskové vzdálenosti objektivu. U zrcadla tedy zdroj nacházející se ve středu křivosti zrcadla (přesněji řečeno ve středu křivosti centrální části zrcadla). Testovací mřížka musí být umístěna do vzdálenosti, pro kterou byl test navržen, tj. zpravidla v definované vzdálenosti před obrazovou rovinou. Při správném umístění by měl pozorovatel v ideálním případě pozorovat rovnoběžné pásy podobně jako u testování sférické plochy. Použití, projevy vad a aberaci i konečná interpretace tohoto testu je pak prakticky shodná s klasickým lineárním testem. V případě jeho použití tedy lze jen s malými omezeními použít závěry uvedené u sférické plochy.
Kruhový test Popov-Terebitz
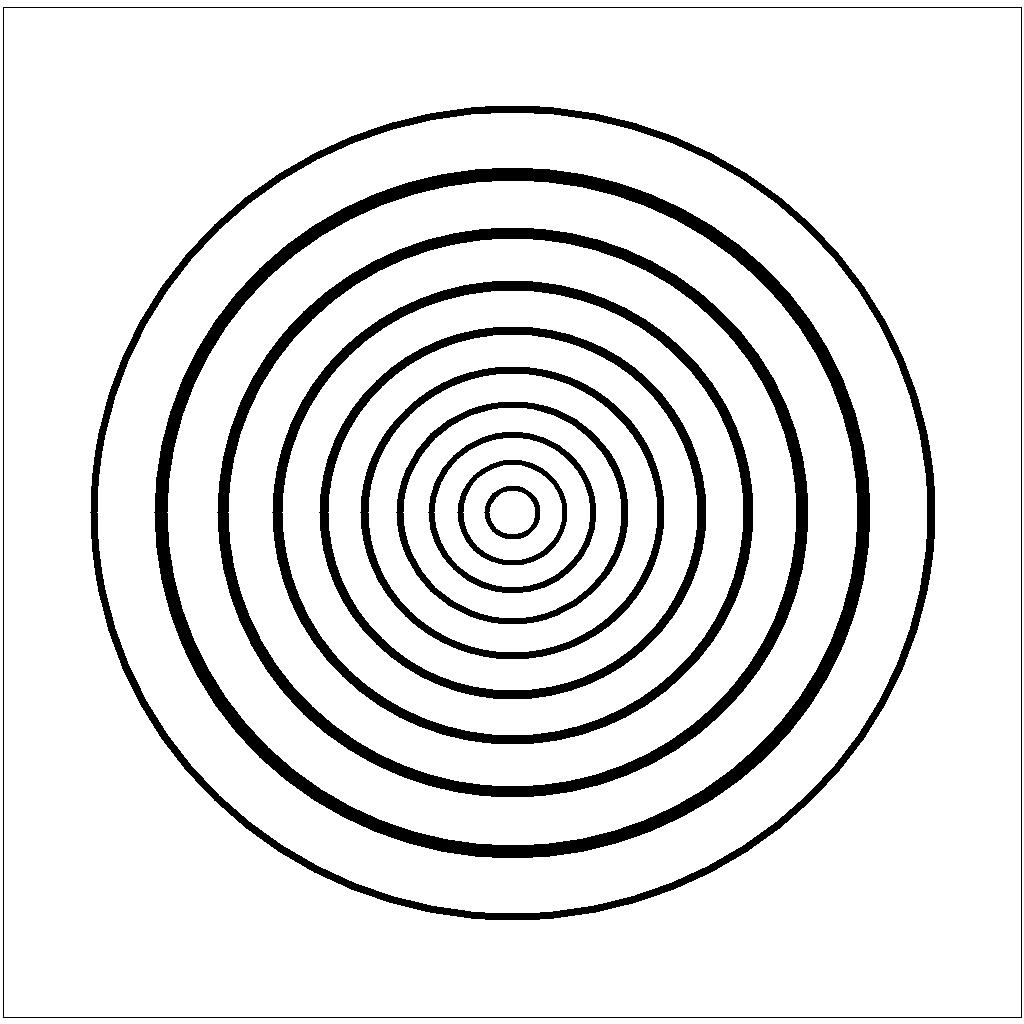
Kruhový test se skládá ze soustředných kružnic, jejichž vzájemná vzdálenost je volena tak, aby při ideální parabolické ploše zrcadla (Popov), popř. při obecně jakékoliv známé excentricitě jeho plochy (Terebitz), pozorovatel viděl v obraze rovnoměrně rozmístěné soustředné kruhy shodné tloušťky.
Prostřednictvím tohoto testu lze velmi dobře testovat lokální deformace zrcadla. Na rozdíl od předchozích testů je možno tento test použít i pro testování nesymetrických aberací, tedy komy a astigmatismu. Vady zrcadla se projeví rozšířením/zúžením šířky pásů, popř. odchylkou od kruhového tvaru. Přítomnost komy se projeví protažením soustředných kružnic pouze v jednom směru od středu testu. Přítomnost astigmatismu pak protažením podél celé jedné osy (namísto kruhu pozorujeme elipsu). Při případném posunu testu podél optické osy směrem k ohnisku se navíc poloha velké osy této elipsy stáčí.
Pro použití tohoto testu platí stejná pravidla jako u testu Mobsby. Test tedy musí být umístěn v definované vzdálenosti od středu křivosti. Nejjednodušším způsobem je nastavit test tak, aby se při jeho zobrazení promítl na zrcadlo předem daný počet kruhů. Rovněž tento test lze nejsnadněji navrhnout existujícími programy (např.již výše uvedený výborný program MODAS).
Během let vznikla celá řada dalších modifikací tohoto testu, které umožňují měření některých specifických vlastností/aberací, popř. optických soustav. Lze tedy říci, že využití Ronchiho testu je dodnes velmi široké.
V příštím pokračování tohoto seriálu se podíváme na další metody testování optických soustav. Zaměříme se opět na některé snadno realizovatelné a dnes mnohdy již téměř zapomenuté metody.
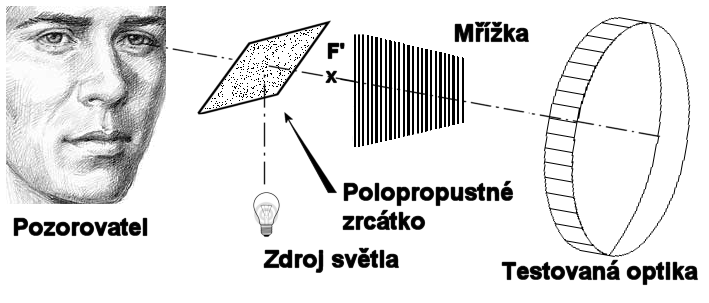
Obr. 1: Základní uspořádání Ronchiho testu


a) b) c)
Obr. 2: Různé varianty Ronchiho testu
a) lineární Ronchiho test,
b) Mobsbyho test navržený pro umístění před obrazovou rovinu,
c) Terebitzův kruhový test.

Obr. 3: Ronchigram ideální sférické plochy
g … hustota mřížky, o … vzdálenost mřížky od obrazové roviny.

Obr. 4: : Ronchigram lineární mřížkou ideální parabolické plochy
g … hustota mřížky, o … vzdálenost mřížky od obrazové roviny.


a) b)
Obr. 5: Probroušený střed
a) mřížka před obrazovou rovinou, b) mřížka za obrazovou rovinou.


a) b)
Obr. 6: Úzká kruhová zóna (prstenec)
a) mřížka před obrazovou rovinou, b) mřížka za obrazovou rovinou.


a) b)
Obr. 7: Sražené okraje
a) mřížka před obrazovou rovinou, b) mřížka za obrazovou rovinou.



a) b) c)
Obr. 8: Ronchigram sférické aberace na kulové ploše
a) mřížka před obrazovou rovinou,
b) mřížka těsně za obrazovou rovinou,
c) mřížka za obrazovou rovinou.


a) b)


c) d)
Obr. 9: Ronchigram komy
a) sfér. plocha, mřížka před obrazovou rovinou,
b) sfér. plocha, mřížka za obrazovou rovinou,
c) parab. plocha, mřížka před obrazovou rovinou,
d) parab. plocha, mřížka za obrazovou rovinou.


a) b)


c) d)
Obr. 10: Ronchigram astigmatismu
a) sfér. plocha, mřížka před obrazovou rovinou,
b) sfér. plocha, mřížka za obrazovou rovinou,
c) parab. plocha, mřížka před obrazovou rovinou,
d) parab. plocha, mřížka za obrazovou rovinou.