V předešlých dílech jsme si uvedli některé nejčastější postupy využívané mezi astronomy amatéry k hodnocení kvality optických přístrojů. Uživatele zpravidla ale příliš nezajímá vlastní kvalita využívaného přístroje, ale spíše kvalita výsledného obrazu. V dnešním, posledním, díle tohoto miniseriálu se zaměříme na komplexní hodnocení kvality soustavy a její vliv na výslednou jakost zobrazení. Řeč bude o přenosové funkci optické soustavy.
Co to je modulační přenosová funkce
Optický signál postupující od pozorovaného objektu do oka pozorovatele (popř. po záznamové médium) je ovlivňován prostředím v němž se tento signál šíří. Prakticky každý pozorovatel velmi dobře zná rušivý vliv atmosféry, která svými vlastnostmi a jevy v ní probíhajícími dokáže značně narušit pozorovanou scénu. Vliv na pozorovaný obraz má samozřejmě i optická soustava přístroje.
Pro jednoduchost předpokládejme místo pozorovaného objektu jednoduchý čárový test tvořený bílými a černými čarami (správně by měl zde být test se sinusovou modulací). V ideálním případě by pozorovatel za optickým přístrojem pozoroval rovněž soustavu bílých a černých pruhů. V reálné situaci nebude ale přechod černá-bílá dokonalý, ale postupný. S rostoucí hustotou čar pak bude sledovaný test pozorován stále méně zřetelně. Test samozřejmě nemusí být tvořen jen prostými čarami, ale např. sinusovým vzorkem.
S druhem a uspořádáním testu souvisí i tzv. modulace. Modulace signálu je v našem případě chápána jako prostorové rozložení jasu v obraze, resp. minimální a maximální intenzita světla (přesněji řečeno je to poměr rozdílu a součtu minimální a maximální intenzity v rámci jedné periody vzorku). V našem případě vzorek s pravoúhlým i se sinusovým průběhem, kde maximum je prezentováno bílou a minimum černou barvou má modulaci (popř. kontrast) rovnu jedné (resp. 100%) .
Přenosem modulace je rozuměn poměr modulace na vstupu optické soustavy ku modulaci téhož signálu na výstupu optické soustavy. Pro jednoduchost nahraďme úroveň jasu bílé jedničkou a černé nulou. Modulace na vstupu je pak rovna (1-0)/(1+0) = 1. Vlivem vlastností optické soustavy bude výstupní modulace nižší, řekněme např. 0.85. Přenos modulace je v našem případě tedy 0.85/1 = 0.85. Pokud nyní budeme měnit hustotu testu obdržíme různé hodnoty přenosu modulace – modulační přenosovou funkci, zkráceně MTF (z angl. Modulation Transfer Function).
Na y-ové ose MTF je přenos modulace, který nabývá hodnot od 0 do 1 (popř. od 0 do 100%). Hodnota rovná 1 (resp. 100%) znamená, že signál se přes optický systém přenesl bez degradace. Hodnota rovna 0 pak signalizuje, že optický signál daných parametrů (tj. i hustoty testu) přes danou optickou soustavu nelze smysluplně přenést. Na x-ové ose je tzv. prostorová frekvence testu (obdoba „klasické“ frekvence v [Hz] používané např. u elektrických signálů) prezentovaná hustotou testu v [period/mm]. U starších měření se můžeme setkat i s jednotkou [čar/mm] (2 čáry jsou rovny jedné periodě testu). Pro přístroje určené k pozorování vzdálených předmětů je pak výhodnější přepočet na úhlové míry [period/rad].
Modulační přenosová funkce lidského oka
Přenosovou funkcí lze popsat samozřejmě nejen optické přístroje, ale např. i lidské oko. Normální lidské oko je za dobrých světelných podmínek schopno rozlišit vzorek černých a bílých čar o úhlové velikosti cca 60“ (tj. 0,000291 rad). Zdravé cvičené oko může být schopno rozpoznat i polovinu této hodnoty. Na druhou stanu za špatných světelných podmínek klesá rozlišovací schopnost lidského oka i na hodnotu 5’ (300“) i hůře. Jednoduchým výpočtem lze pak zjistit hustotu čárového testu v konvenční vzdálenosti lidského oka (tj. vzdálenost, na kterou je schopno průměrné oko ještě zaostřit, je rovna 25cm) a při standardní ohniskové vzdálenosti čočky lidského oka (16,7 mm). Pro dobré světelné podmínky obdržíme hodnotu 6,88 period/mm (tzn. párů čar na mm), resp. pro vzdálené objekty 0,58 period/mrad. Jinak řečeno – na vzdálenost 25 cm je lidské oko schopno rozpoznat zpravidla detail cca 0,15 mm. To samozřejmě platí jen za dobrých světelných podmínek a při modulaci (resp. kontrastu objekt/pozadí) rovnému jedné. Modulace (resp. kontrast objekt/pozadí) takto pozorovaného detailu (resp. soustavy čar) již ale nebude roven jedné, ale bude mít minimální hodnotu nutnou k jeho rozlišení. Úhlově větší detaily jsou pak zobrazeny s modulací mezi touto minimální a ideální (1,0) hodnotou. Typický průběh MTF lidského oka je ukázán na obrázku níže.
Interpretace modulační přenosová funkce
Kontrast/brilance, ostrost obrazu
Modulační přenosová funkce je jednou z nejlepších charakteristik popisujících kvalitu přístroje. Lze z ní přímo vyčíst, popř. odvodit, celou řadu základních vlastností příslušné optické soustavy. Průběh MTF není bohužel shodný pro celé zorné pole. Pro úplnost je nutno dodat, že průběh MTF nemusí být obecně zcela totožný ani pro dva na sebe kolmé směry v témže místě zorného pole.
Nejjednodušší je situace u soustav s velmi malým zorným polem. Této podmínce vyhovuje velká část astronomických dalekohledů. V tomto případě je pokles průběhu MTF v okrajích velmi malý a soustavu lze souhrnně popsat klasickým průběhem MTF tak, jak je popsán výše.
Složitější situace je u soustav s větším zorným polem (např. fotoaparáty, dalekohledy s velkým relativním otvorem). Zpravidla nejblíže ideálnímu bývá průběh MTF v okolí středu (optické osy) a směrem k okrajům se jeho průběh zhoršuje. Pro popis těchto systémů je vhodnější prezentaci MTF upravit. Na rozdíl od předchozího případu není na x-ové ose rostoucí prostorová frekvence. Pro test je využit rastr z normovanou hustotou čar a je zkoumáno, s jakým výsledným kontrastem je tento test zobrazen v různých částech zorného pole. Na x-ové ose je proto vynesena vzdálenost zobrazení od optické osy, popř. přímo příslušná hodnota zorného pole. Standardní hustota používaného testu je definována pro potřeby fotografické techniky. Je zpravidla 10 period/mm (v některých případech jen 5 period/mm) a 40 period/mm (občas i 30-70 period/mm). Pro potřeby astronomů je občas nutné využít testy s vyšší hustotou.
V případě testu 10 period/mm se výsledný graf nazývá kontrastem obrazu. Jde o trošku nešťastně zvolenou terminologii, kdy je nutno odlišit od původního významu slova kontrast používaného v optice (poměr jasu objektu k jasu pozadí). Proto je vhodné využívat i druhý název – brilance obrazu. Pozorovatel je schopen v obraze rozlišit i velmi malé rozdíly (i 2,5%). Dobrá optická soustava má mít hodnotu kontrastu/brilance obrazu přes 95%.
Při použití testu s vyšší hustotou (40 period/mm) pak hovoříme o ostrosti obrazu. Ostrost obrazu nese informaci, jak kvalitně jsou zobrazeny velmi jemné struktury. Oproti kontrastu/brilanci obrazu nejsou již rozpoznatelné malé rozdíly. např. při hustotě testu 40 period/mm nejsou zpravidla pozorovatelné rozdíly v zobrazení testu i 10%. Z obrázku níže je patrné, že ostrost obrazu bezpodmínečně nevyžaduje vysoký kontrast/brilanci obrazu.
Je to možná trošku udivující, ale zobrazení objektivu, který má obraz s velkým kontrastem/brilancí a menší ostrostí, je vnímáno okem pozorovatele ostřeji než u objektivu s větší ostrostí a menším kontrastem/brilancí obrazu. Optimální je samozřejmě optická soustava s vysokým kontrastem/brilancí i ostrostí zobrazení.
Rozlišovací schopnost, difrakční limit
V ideálním případě by MTF představovala křivka rovnoběžná s osou x a protínající osu y v hodnotě jedna (resp. 100%). Ideální optická soustava (tj. soustava bez optických aberací) je oproti tomuto ideálnímu stavu omezena i difrakčními limity. Soustava s menší vstupní aperturou (menším průměrem objektivu) bude popsána křivkou, která klesá k nulovým hodnotám rychleji než soustava s větší vstupní aperturou. S rostoucím průměrem vstupní apertury roste rozlišovací schopnost této soustavy a klesá průměr Airyho disku. Průběh křivky MTF ideální optické soustavy se pak oproti ideálnímu případu od určité prostorové frekvence klesá a přibližuje se k nulové hodnotě. Na Airyho disk můžeme pohlížet i coby obdobu/segment čárového testu. V obrazové rovině objektivu je jeho velikost rovna převrácené hodnotě hustoty ekvivalentního čárového testu.
Průběh reálné optické soustavy se bude svým průběhem v závislosti na její kvalitě více či méně blížit průběhu ideální optické soustavy. Čím bude průběh křivky MTF bližší ideálnímu, tím kvalitnější tím kvalitnější bude i soustava. V klasickém tvaru (tj. s prostorovou frekvencí popř. hustotou testu na x-ové ose) poklesne MTF v určitém místě grafu na minimální přípustnou úroveň. Pro lidské oko je tato hodnota dána prahovým kontrastem lidského oka – tj. 0.02. Pro jiné detekční systémy může být tato hodnota jiná a pohybuje se zpravidla v rozmezí 0,005 až 0,1. Příslušná x-ová hodnota se pak nazývá mezní frekvencí. Převrácená hodnota této frekvence charakterizuje rozlišovací schopnost soustavy.
MTF je sice jednou z nejuniverzálnějších charakteristik optické soustavy, nicméně ji nelze považovat za „všeobsahující“. Např. distorze, zklenutí obrazového pole či vinětace nejsou přímo z jediné MTF určitelné. Rovněž pro stanovení zbytkové barevné vady je nutno stanovit průběh MTF pro různé vlnové délky. Nekvalitní antireflexní vrstvy se u refrakční optiky projeví poklesem kontrastu zobrazení často bez zhoršení mezní frekvence (resp. rozlišovací schopnosti).
Na druhou stranu lze z průběhu MTF velmi dobře určit např. astigmatismus. Při testování optické soustavy k tomu postačí dva testy otočené o 90°. Pokud křivky zjištěné MTF se vůči sobě výrazněji rozbíhají, signalizuje to právě potíže s astigmatismem.
Vliv centrálního stínění
Modulační přenosová funkce ideální difrakčně omezené optické soustavy tak jak je popsána výše platí pro soustavu bez centrálního stínění – tedy pro refraktory. Velká část astronomických dalekohledů je ale tvořena zrcadlovými soustavami, u nichž často sekundární zrcátko stíní část primárního zrcadla. velikost tohoto stínění lze vyjádřit coby poměr průměru sekundárního a primárního zrcadla (tzv. koeficient centrálního stínění).
V obrazu hvězdy (resp. v jeho difrakčním obrazci) se vliv centrálního stínění projeví snížením intenzity centrálního Airyho disku a přesunem energie z něj do soustředných kruhů.
Toto stínění se přirozeně projeví i ve výsledném tvaru křivky MTF. Ideální difrakčně omezená optická soustava s centrálním stíněním má MTF jejíž průběh je v oblasti nižších a středních prostorových frekvencí pod průběhem obdobné ideální optické soustavy bez centrálního stínění. Velikost tohoto poklesu je tím větší, čím je větší centrální stínění. V oblasti vysokých prostorových frekvencí může naopak docházet k jejich zvýšení i nad úroveň ideální optické soustavy bez centrálního stínění. Hodnota mezní frekvence (a tím i rozlišovací schopnost) se přitom nemění. Při pozorování jasných a kontrastních objektů (např. Měsíc, kotoučky planet, prstence Saturnu včetně Cassiniho dělení), kdy je hlavním kritériem rozlišovací schopnost přístroje jsou proto soustavy s centrálním stíněním plně srovnatelné se soustavami bez centrálního stínění stejných parametrů.
Řada astronomů amatérů považuje za jeden z hlavních kritérií kvality jejich přístroje právě rozlišovací schopnost. Z uvedeného je patrné, že takto pojatá kvalita optického přístroje není limitována jeho centrálním stíněním. V reálných situacích ji mnohem více ovlivňují okolnosti spjaté s provozem přístroje – tepelné vyrovnání optiky, ale i mechanických částí, přesnost a stabilita zaostření, stabilita mechanických komponent v nichž je uložena optika, ...
Z výše uvedeného popisu je patrný i vliv centrálního stínění na výsledný obraz. Soustava s centrálním stíněním bude obraz zobrazovat s nižším kontrastem/brilancí. Přírůstek ostrosti zobrazení je zpravidla velmi malý až nepozorovatelný. Pro koeficient centrálního stínění pod cca 0,2 (tj. 20%) je vliv centrálního stínění prakticky zanedbatelný. Pro koeficient centrálního stínění pod cca 0,33 (tj. 33%) je můžeme považovat za malý. K výraznému poklesu kontrastu obrazu dochází až u soustav s centrálním stíněním nad cca 0,4-0,6 (tj. 40-60%). Pro zobrazení málo výrazných (tj. málo kontrastních) prvků jako jsou např. detaily na povrchu planet je proto výhodnější využít optickou soustavu bez centrálního stínění. Využití optických soustav bez centrálního stínění je důležité zejména v situacích, kdy je pozorován detail jehož kontrast je jen o málo vyšší než je prahový kontrast lidského oka (popř. použitého detekčního systému). V opačném případě nemusí být detail rozpoznán.
Zjednodušeně lze říci, že kontrast zobrazení ideální optické soustavy s centrálním stíněním s průměrem hlavního zrcadla D a sekundárního d je přibližně roven kontrastu zobrazení ideální optické soustavy bez centrálního stínění o průměru D-d. Přibližné průměry ideálních optických soustav s a bez centrálního stínění pro dosažení stejného kontrastu/brilance zobrazení jsou uvedeny v tab. 1. Tato tabulka je pouze orientační. Reálná optická soustava se může přirozeně lišit.
Tab. 1: Ekvivalentní průměry objektivu u soustav s a bez centrálního stínění .
|
Průměr objektivu OS [mm] |
||||
|
bez centrál. stínění |
s centrál. stíněním 15% |
s centrál. stíněním 30% |
s centrál. stíněním 45% |
s centrál. stíněním 60% |
|
100 |
85 |
70 |
60 |
40 |
|
150 |
127 |
100 |
80 |
60 |
|
200 |
170 |
140 |
100 |
80 |
|
250 |
210 |
170 |
120 |
100 |
|
300 |
250 |
210 |
140 |
120 |
|
350 |
300 |
250 |
210 |
140 |
Určení modulační přenosová funkce
Pro určení MTF je vhodné využít některý ze standardizovaných testů. Příkladem vhodných čárových testů je např. čárový test označovaný USAF-1951 a KOREN-2003 a tzv. Siemensova hvězda.
V praxi se často uspořádávají jednotlivé testy tak, aby bylo jediným měřením pokryto celé zájmové (zorné) pole. Jsou tedy umístěny ve středu i okrajích zorného pole, popř. i v jeho částech (polovině, třetině, …).
Test USAF-1951
Test USAF-1951 byl původně definován americkou vojenskou normou MIL-STD-150A. Velmi záhy se však rozšířil i do civilní praxe a dnes je široce využíván pro testy optických přístrojů (dalekohledů, fotoaparátů, mikroskopů). Je primárně určen k určení rozlišovací schopnosti soustavy. Je tvořen soustavou několika skupin elementárních testů. V každé skupině je šest elementárních různě velkých o 90° pootočených dvojic čárových testů. Jednotlivé testy v rámci skupiny mají vůči sobě přesně definovanou velikost. Jednotlivé skupiny vůči sobě pak umístění v celém testu. Skupiny s nižším hustotou čar jsou umístěny vně, skupiny s vyšší hustotou čar u středu testu. To umožňuje určit najednou průběh MTF pro oba na sebe kolmé směry (sagitální i meridiální). Platí, že velikost prvního testu ve skupině má vždy poloviční velikost než test skupiny předešlé.
Při dodržení těchto rozměrů je nutné umístit tento test do vhodné vzdálenosti. Tu lze určit pomocí jednoduchého pravidla - na každý milimetr ohniskové délky objektivu je nutné počítat 1 palec (25,4 mm) vzdálenosti. Objektivu o ohniskové vzdálenosti např. 1m tak odpovídá vzdálenost testu 25,4 m. Pozorovaná rozlišovací schopnost prvních testů ve skupinách je pak uvedena v tab. 4. V případě potřeby např. dvojnásobného rozlišení postačuje vyrobit test dle rozměrů z tab. 2 dělených dvěma, popř. jej umístit do dvojnásobné vzdálenosti.
Tab. 2: Měřítko jednotlivých testů uvnitř jedné skupiny testu USAF-1951
|
Test ve skupině |
Násobitel (přesně) |
Násobitel (číslo) |
|
1 |
20 |
1.00000 |
|
2 |
2-1/6 |
0.89090 |
|
3 |
2-2/6 |
0.79370 |
|
4 |
2-3/6 |
0.70711 |
|
5 |
2-4/6 |
0.62996 |
|
6 |
2-5/6 |
0.56123 |
Tab. 3: Příklad rozměrů testu USAF-1951
|
|
Elementární test |
|||||
|
Skupina |
1 |
2 |
3 |
4 |
5 |
6 |
|
-2 |
10.00000 |
8.90899 |
7.93701 |
7.07107 |
6.29961 |
5.61231 |
|
-1 |
5.00000 |
4.45449 |
3.96850 |
3.53553 |
3.14980 |
2.80616 |
|
0 |
2.50000 |
2.22725 |
1.98425 |
1.76777 |
1.57490 |
1.40308 |
|
1 |
1.25000 |
1.11362 |
0.99213 |
0.88388 |
0.78745 |
0.70154 |
|
2 |
0.62500 |
0.55681 |
0.49606 |
0.44194 |
0.39373 |
0.35077 |
|
3 |
0.31250 |
0.27841 |
0.24803 |
0.22097 |
0.19686 |
0.17538 |
|
4 |
0.15625 |
0.13920 |
0.12402 |
0.11049 |
0.09843 |
0.08769 |
Tab. 4: Hustota elementárních testů
|
|
Délka čáry prvního elementu skupiny |
Hustota testu [čar/mm] |
|
-2 |
10.000 |
0.25 |
|
-1 |
5.0000 |
0.50 |
|
0 |
2.5000 |
1 |
|
1 |
1.2500 |
2 |
|
2 |
0.62500 |
4 |
|
3 |
0.31250 |
8 |
|
4 |
0.15625 |
16 |
|
5 |
0.078125 |
32 |
Test lze využít i k přibližnému určení MTF. V tomto případě můžeme pominout rozdíl mezi sinusovým a čárovým vzorkem testů, resp. mezi modulací a kontrastem.Vlastní určení MTF spočívá v záznamu celého testu a určení kontrastů, s nimiž jsou jednotlivé testovací obrazce vykresleny. Pro stanovení korektního průběhu křivky MTF zpravidla postačuje vyhodnotit test odpovídající zjištěné rozlišovací schopnosti a další čtyři elementární testy (z toho alespoň 1-2 v přechodové oblasti). Následné zjištěné kontrasty testů je nutno před vynesením do grafu vynásobit koeficientem 0,785 (/4). Pokud by byly vyneseny hodnoty kontrastu určené z pravoúhlého čárového testu přímo bez násobení opravným koeficientem, obdrželi bychom tzv. přenosovou funkci kontrastu (CTF) nikoliv MTF. Na ose x je hustota příslušného testu ([period/mm]). Na y-ovou osu jsou vyneseny příslušné opravené hodnoty kontrastu bílá-černá čára.
Test KOREN 2003
Uvedená verze testu byla navržena Normanem Korenem v roce 2003. Na rozdíl od testu USAF-1951 tento test již dopředu počítá s určováním MTF. Proto umožňuje její přesné určení i pro velké prostorové frekvence (nad 100 period/mm).
Test se skládá z šesti základních pásů. Základními je čárový test a test se sinusovým vzorkem. Hustota obou typů testů se postupně zvyšuje od 2 po 200 period/mm. Sinusový test je určen ke stanovení průběhu MTF. Čárový test pak pro určení úrovně zaostření obrazu. S výhodou lze využít skutečnosti, že pravoúhlý čárový test je rozlišitelný do vyšších prostorových frekvencí (cca o 27%) než sinusový test. Pří ostření stačí sledovat tento pás a doostřit tak, aby byla rozlišitelná co nejvyšší prostorová frekvence. Samozřejmě je možno jej využít i k určení MTF. V tomto případě ale platí poznámka o násobení koeficientem 0,785 uvedená u testu USAF-1951.
Zbývající pásy v testu obsahují konstantní prostorovou frekvenci se sinusovým test s kontrastem 50% (s hodnotami mezi 25 a 75% max. hodnoty) a 10% (s hodnotami mezi 45 a 55%). Tyto pásy jsou využívány jen při vizuálním vyhodnocení testu pro přímé porovnání pozorovatelného kontrastu s vyhodnocovaným pásem (sinusový pás s 100% kontrastem).
Obecný postup použití tohoto testu je podobný jako v předchozím případě testu USAF-1951. Spočívá v několika základních krocích:
-
Sestavení testovacího obrazce z dílčích testů. Zpravidla se umisťují vždy dva na sebe kolmé tesy do středu, poloviny a kraje zorného pole.
-
Umístění testu do vhodné vzdálenosti a záznam odezvy testu (např. odfotografováním)
-
Vyhodnocení odezvy dílčích testů.
.Podrobný postup určení MTF s využitím tohoto testu je popsán na webových stránkách autora testu (www.normankoren.com). Zde rovněž naleznete i vyhodnocovací software pro stanovení výsledné MTF a vlastní test pro různé typy tiskáren..
Siemensova hvězda
Siemensova hvězda patří mezi astronomy amatéry mezi neprávem opomíjené testy. Starší generace jej možná zná pod názvem Jewellův test. Kruhová plocha testu je rozdělena na definovaný počet stejných výsečí střídavě bílých a černých. Tvoří tak obdobu čárového testu. Modulace jednotlivých výsečí může být jak pravoúhlá (tj. ostré přechody černá-bílá), popř. sinusová.
Pravoúhlé modulace se využívá zejména k určení rozlišovací schopnosti optické soustavy. Pozorovatel při sledování testu vidí uprostřed kruhového testu nerozlišenou oblast (šedou plochu). Průměr této plochy je přímo úměrný rozlišovací schopnosti. Např. pro Siemensovu hvězdu o 72 výsečích pak pro rozlišovací schopnost platí jednoduchý vztah =18d/L (kde d je průměr nerozlišené plochy v [mm] a L vzdálenost testu v [m]). nerozlišená plocha by přitom měla být kruhová. Pokud má tvar v nějakém směru protáhlejší (elipsy), signalizuje to potíže optického systému s astigmatismem.
Tento test lze samozřejmě využít i k určení MTF optického systému (viz. poznámka u testu USAF-1951. Pro její určení je ale výhodnější použít Siemensovu hvězdu se sinusovou modulací výsečí. V tomto případě je vhodné umístit pro přesné zaostření optického systému do středu testu malou Siemensovu hvězdu s 4 výsečemi. Její velikost je nutné volit tak, aby celá ležela v nerozlišené části testu. Minimální testovaná prostorová frekvence je dána průměrem Siemensovy hvězdy a počtem těchto segmentů. Směrem do středu Siemensovy hvězdy pak pozorovaná prostorová frekvence roste. Nevýhodou tohoto testu je, že je jej nutno vyhodnocovat. v polárních souřadnicích s počátkem ve středu testu (tzn. v soustředných kruzích). výhodou na druhou stranu je, že zatímco test USAF-1951 umožňuje určovat rozlišovací schopnost a MTF ve dvou na sobě kolmých směrech, Siemensovu hvězda je vhodná pro určování MTF v libovolném směru obrazového pole.
Závěr
Zaměření posledního dílu seriálu bylo úmyslně nasměrováno na přenosovou funkci optické soustavy. Celá řada astronomů má již při vyslovení jejího názvu neopodstatněné obavy a pocit čehosi tajemného, popř. až příliš vědeckého. Přitom právě MTF popř. koeficienty z ní odvozené (SR koeficient) dokáže asi nejlépe postihnout kvalitu optického systému. Cílem tohoto článku tedy bylo vysvětlit alespoň některé základní pojmy a zejména pomoci ji správně interpretovat.
V našem krátkém seriálu jsme si ukázali nejčastější postupy hodnocení kvality optických přístrojů. Rovněž jsme si naznačili některé užitečné postupy pro jejich realizaci. Během psaní tohoto seriálu byla shromážděna celá řada dotazů. Velká část z nich se týkala konkrétních realizací testů, popř. žádostí o radu jak orientačně rychle rozpoznat nekvalitní optiku. Na některé z těchto nejčastějších bude určitě zaměřen v budoucnosti samostatný článek.



a) b) c)
Obr.1: Jednoduchý čárový test;
a) původní test,
b) test po průchodu optickou soustavou,
c) diskrétní sinusový čárový test (16 úrovní šedé).
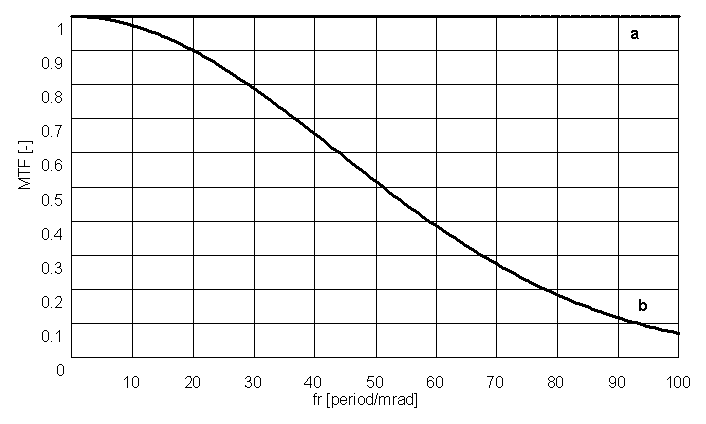
Obr. 2: Modulační přenosová funkce;
a) ideální MTF, b) MTF ideální optické soustavy (bezaberační, difrakčně omezené).
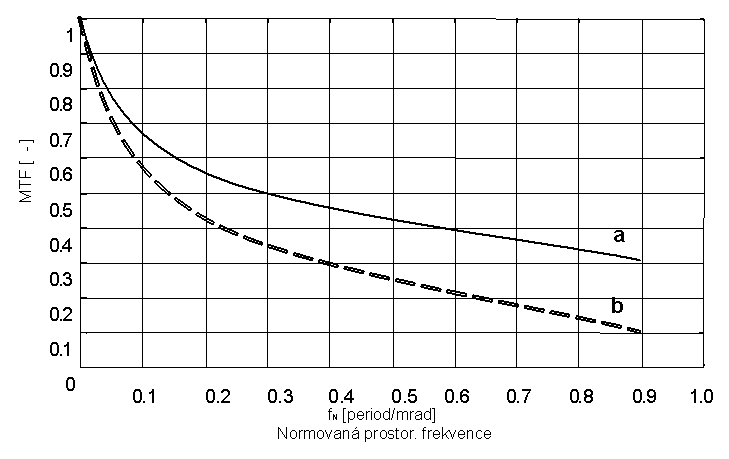
Obr. 3: Modulační přenosová funkce lidského oka;
a) průměr zřítelnice 6mm, b) průměr zřítelnice 2 mm.



a) b) c)
Obr. 4: Vliv centrálního stínění na difrakční obrazec hvězdy
a) soustava bez centrálního stínění,
b) soustava s koeficientem centrálního stínění 30%,
c) soustava s koeficientem centrálního stínění 60%.
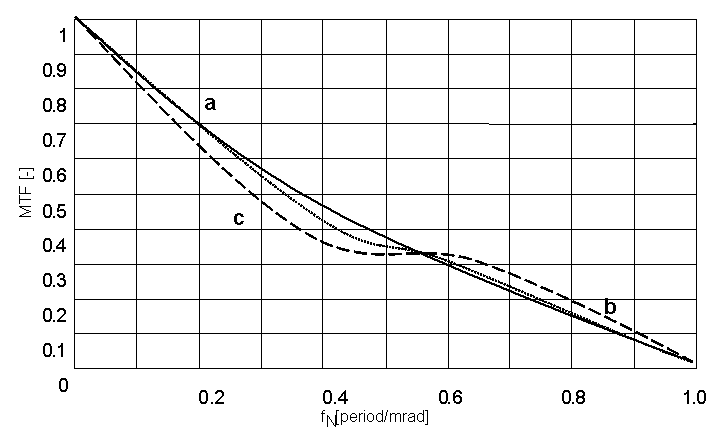
Obr. 5: Vliv centrálního stínění na tvar MTF;
a) soustava bez centrálního stínění,
b) soustava s centrálním stíněním 20%,
c) soustava s centrálním stíněním 40%.
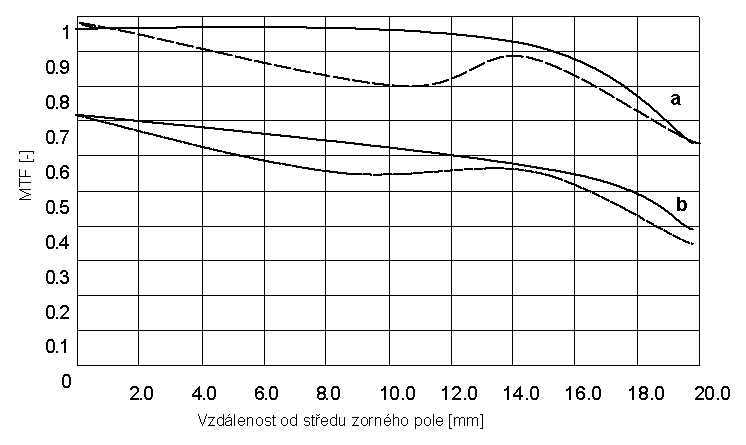
Obr. 6:Kontrast/brilance a ostrost zobrazení;
a) kontrast zobrazení (plně – tangenciální směr, čárkovaně - meridiální),
b) ostrost zobrazení (plně – tangenciální směr, čárkovaně - meridiální),




a) b) c) d)
Obr. 7: Vliv kontrastu/brilance a ostrosti zobrazení na výsledný obraz.
a) dokonalý kontrast/brilance obrazu i ostrost,
b) vysoký kontrast/brilance obrazu, horší ostrost,
c) horší kontrast/brilance obrazu, vysoká ostrost,
d) nízký kontrast/brilance obrazu i ostrost,
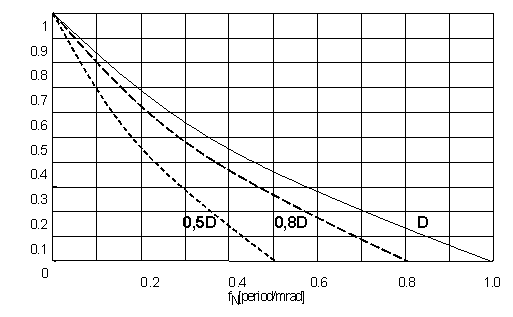
Obr. 8: Průběhy MTF ideální optické soustavy pro různé průměry vstupní apertury.
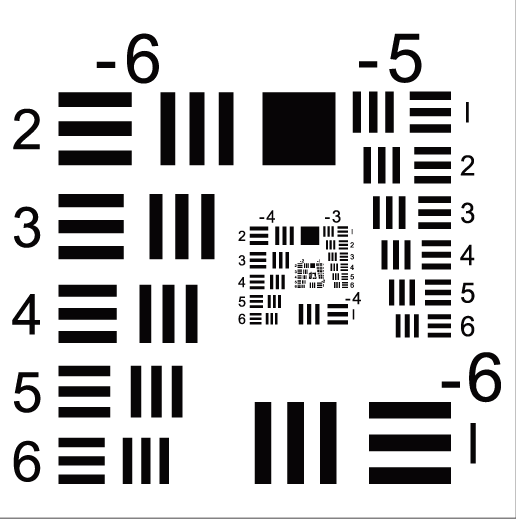
Obr. 9: Čárový test USAF-1951

Obr. 10: Test KOREN-2003

Obr. 11: Siemensova hvězda